V této kapitole si vysvětlíme, jak zobrazit tělesa. Začneme hranatými tělesy, poté ukážeme tělesa rotační.

Podstavy těles budeme umisťovat do půdorysny. Druhá podstava hranolu nebo válce bude v rovině rovnoběžné s půdorysnou. Tělesa s podstavou v nárysně (resp. v bokorysně) se zobrazí obdobně jako tělesa s podstavou v půdorysně: je třeba zobrazit podstavu tělesa v dané rovině, u hranolů a válců i v rovině rovnoběžné (viz podkapitoly 6.2, 7.5). Tělesy s podstavou v ostatních rovinách se zabývat nebudeme.

Tělesa budeme umisťovat zpravidla do prvního oktantu.

8.1 Hranol

K zobrazení hranolu je třeba zobrazit jeho podstavy a úsečkami správně spojit jednotlivé vrcholy těchto podstav. Musíme tedy umět zobrazit mnohoúhelník (podstavu) v půdorysně a v rovině rovnoběžné s půdorysnou (viz kapitola 6). Na obr. 8.1 vidíme pětiúhelníky \(ABCDE\) a \(A'B'C'D'E'\) jako podstavy kolmého hranolu. Hranol \(ABCDEA'B'C'D'E'\) dokončíme sestrojením úseček \(AA'\), \(BB'\), \(CC'\), \(DD'\), \(EE'\).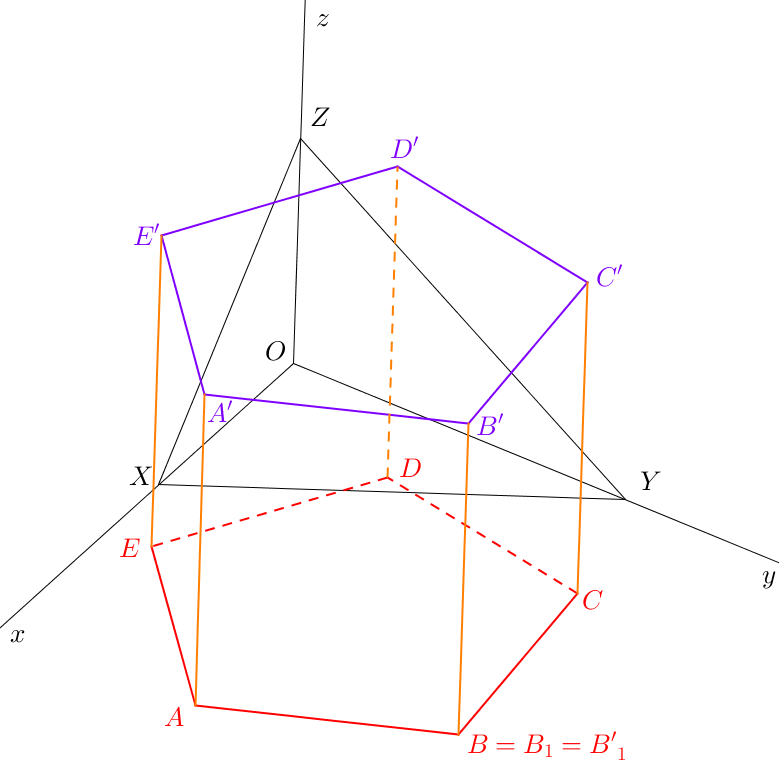

V obrázku 8.1 jsou popsány axonometrické půdorysy bodů \(B\), \(B'\). Pro lepší přehlednost obvykle nepopisujeme axonometrické půdorysy všech bodů.

Dále je třeba vyřešit viditelnost hran. Můžeme začít konvexní obálkou všech vrcholů tělesa, která je vždy vidět. Úsečky \(AB\), \(BC\), \(CC'\), \(C'D'\), \(D'E'\), \(E'E\), \(EA\) tedy budou vidět (spojíme plnými čarami). Také víme, že horní podstava bude vidět. Hrany \(E'A'\), \(A'B'\), \(B'C'\) proto rovněž spojíme plnými čarami. Jelikož je hrana \(AA'\) ohraničená dvěma viditelnými vrcholy, bude i tato hrana viditelná. Stejně tak hrana \(BB'\) bude vidět. Zbylé hrany \(CD\), \(DE\), \(DD'\) již vidět nebudou, spojíme je tedy čárkovanými čarami.

Obdobný postup řešení viditelnosti hran lze použít u dalších těles. Při zobrazování dalších těles v tomto textu se viditelností zabývat nebudeme. Nesmíme na ni ale zapomínat.

Úloha 37. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(A=[0;4;3]\), \(S=[0;4;6]\). Sestrojte pravidelný šestiboký hranol \(ABCDEFA'B'C'D'E'F'\), jehož podstava leží v bokorysně. Bod \(S\) je střed podstavy, výška hranolu \(v = 7\). Hranol leží v prvním oktantu. ŘEŠENÍ

Úloha 38. \(X\)[11; 4-18], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=5\). Jsou dány body \(A=[2;0;5]\), \(B=[9;0;9]\), \(C=[5;0;4]\), \(D=[3,0,4]\), \(E=[1;0;1]\) a délka \(v=5\). Sestrojte kolmý hranol \(ABCDEA'B'C'D'E'\), jehož výška je \(v\). Hranol leží v prvním oktantu.

Kosý hranol zobrazíme obdobným způsobem jako kolmý (viz obr. 8.2). Nejprve sestrojíme obě podstavy, které pospojujeme vhodnými úsečkami. Nakonec vyřešíme viditelnost.

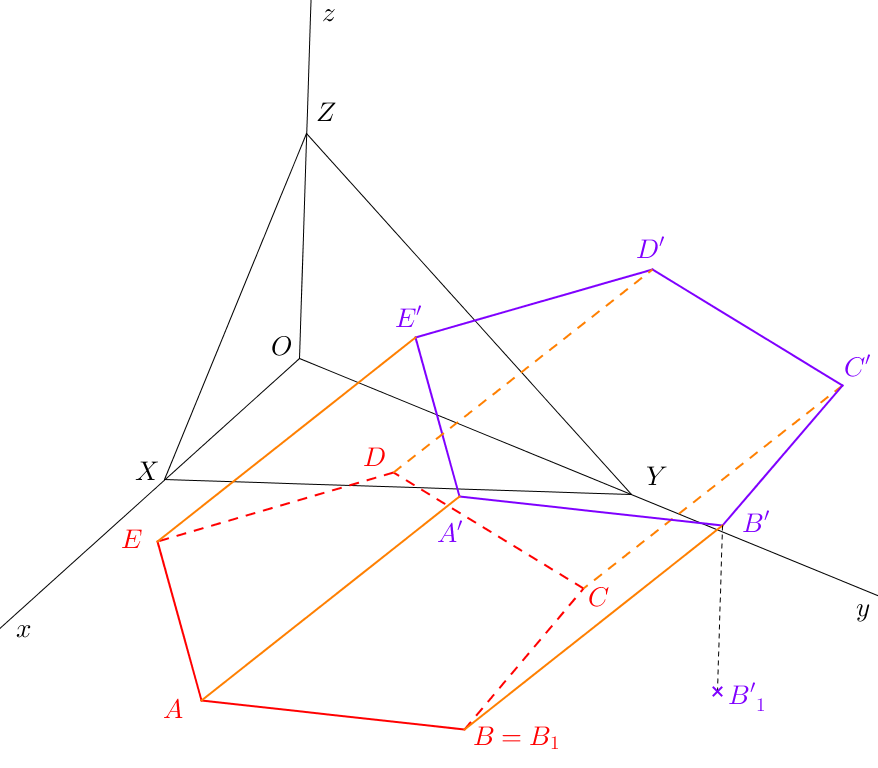
Úloha 39. \(X\)[4-10; 10-20], \(\triangle XYZ\): \(|XY|=7\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(A=[6;1;0]\), \(B=[8;0;0]\), \(C=[9;8;0]\), \(A'=[7;9;8]\). Sestrojte kosý hranol \(ABCA'B'C'\).

8.2 Jehlan

V případě jehlanu zobrazíme nejprve jeho podstavu. Dále sestrojíme hlavní vrchol, který spojíme úsečkami (bočními hranami jehlanu) se všemi vrcholy podstavy. Nakonec vyřešíme viditelnost (obr. 8.3).

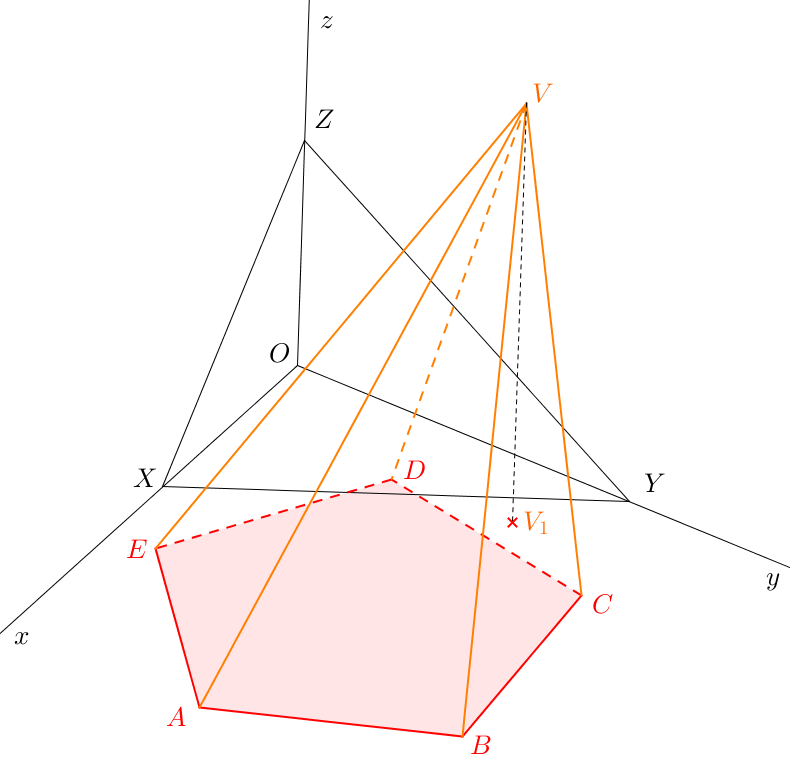
Úloha 40. \(X\)[5-13; 3-20], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Jsou dány body \(A=[4;0;3]\), \(B=[1;0;6]\). Sestrojte pravidelný trojboký jehlan \(ABCV\) s podstavou v nárysně. Výška jehlanu \(v = 7\). Jehlan leží v prvním oktantu. ŘEŠENÍ

Úloha 41. \(X\)[5-9; 3-21], \(\triangle XYZ\): \(|XY|=7\), \(|YZ|=8\), \(|XZ|=8\). Jsou dány body \(A=[8;0;3]\), \(B=[2;0;2]\), \(C=[0;0;9]\), \(D=[7;0;8]\), \(E=[4;0;7]\), \(F=[3;0;4]\), \(V=[1;10;9]\). Sestrojte jehlan \(ABCDEFV\).

8.2.1 Komolý jehlan

Komolý jehlan (obr. 8.4) zobrazíme stejným způsobem jako hranol: začneme podstavami tělesa, které spojíme příslušnými hranami, a poté vyřešíme viditelnost. Na první pohled může být náročnější zobrazení horní podstavy. Zatímco u hranolu vznikne horní podstava posunutím dolní podstavy, u komolých jehlanů to funguje jinak.

Máme-li zadanou dolní podstavu, horní podstava může být určena např. jedním z vrcholů podstavy a délkou hrany podstavy, která z tohoto vrcholu vychází (např. bod \(A'\) a velikost hrany \(A'B'\) na obr. 8.4). V tomto případě sestrojíme bod \(B'\) a přímky \(AA'\), \(BB'\). Poté získáme vrchol jehlanu \(V\) jako průsečík \(AA'\), \(BB'\). Víme, že body \(C'\), \(D'\), \(E'\) leží po řadě na přímkách \(CV\), \(DV\), \(EV\) a hrany \(B'C'\), \(C'D'\), \(D'E'\), \(E'A'\) jsou rovnoběžné s hranami \(BC\), \(CD\), \(DE\), \(EA\).

I v případě jiného zadání komolého jehlanu vycházíme při konstrukci podstav vždy ze stejnolehlosti, která má následující vlastnosti:

• všechny přímky \(AA'\), \(BB'\), ... (prodloužené boční hrany) se protínají v jednom bodě,
• hrany \(AB\), \(BC\), ... jsou rovnoběžné s hranami \(A'B'\), \(B'C'\), ...

Úloha 42. \(X\)[10; 4-21], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=8\), \(|XZ|=8\). Jsou dány body \(A=[0;3;8]\), \(B=[0;2;0]\), \(C=[0;0;7]\), \(A'=[8;1;4]\) a vzdálenost \(|A'B'|=4\). Sestrojte komolý jehlan \(ABCA'B'C'\).

8.3 Rotační válec

Chceme-li zobrazit rotační válec (obr. 8.5), zobrazíme nejprve jeho kruhové podstavy, jejichž axonometrickými průměty jsou části rovin vymezené elipsami. (Konstrukce kružnice v půdorysně viz kapitola 7.) Dále sestrojíme obrysové površky válce, které se zobrazí jako tečny k podstavám ve směru průmětu osy válce.

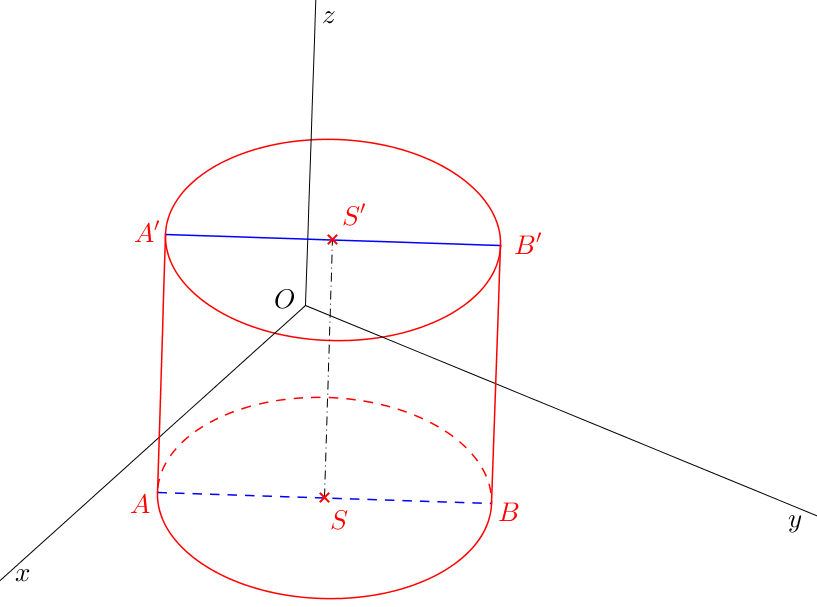
Nakonec vyřešíme viditelnost. Podstava ležící v rovině rovnoběžné s půdorysnou a obrysové površky budou vidět. Část podstavy v půdorysně tvořící konvexní obálku (je ohraničená dotykovými body obrysových površek) je viditelná, zbylá část je neviditelná. V prvním oktantu platí uvedený postup pro všechny válce.

Úloha 43. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán bod \(S=[8;8;0]\) a délky \(r=3\), \(v=7\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v půdorysně. Výška válce je \(v\). Válec leží v prvním oktantu. ŘEŠENÍ

Úloha 44. \(X\)[2-11; 2-18], \(\triangle XYZ\): \(|XY|=8\), \(|YZ|=9\), \(|XZ|=6\). Je dán bod \(S=[0;1;0]\) a délky \(r=3\), \(v=7\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v půdorysně. Výška válce je \(v\). Válec leží v prvním oktantu.

8.4 Rotační kužel

Při zobrazení rotačního kužele (obr. 8.6) sestrojíme nejprve jeho podstavu (viz podkapitola 8.3) a hlavní vrchol \(V\). Obrysovými přímkami jsou tečny k průmětu podstavy z průmětu vrcholu kužele, tj. tečny z bodu k elipse.

Viditelnost určíme stejně jako u válců: obrysové površky jsou viditelné, podstava je z části neviditelná. (V prvním oktantu platí vždy.)

Úloha 45. \(X\)[3-9; 2-18], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán bod \(S=[0;0;0]\) a délky \(r=3\), \(v=10\). Sestrojte rotační kužel, jehož podstava se středem \(S\) a poloměrem \(r\) leží v půdorysně. Výška kužele je \(v\). Kužel leží v prvním oktantu. ŘEŠENÍ

Úloha 46. \(X\)[2-11; 2-21], \(\triangle XYZ\): \(|XY|=5\), \(|YZ|=7\), \(|XZ|=8\). Je dán bod \(S=[0;0;5]\) a délky \(r=2\), \(v=5\). Sestrojte rotační kužel, jehož podstava se středem \(S\) a poloměrem \(r\) leží v nárysně. Výška kužele je \(v\). Kužel leží v prvním oktantu.

8.5 Koule

Průmětem koule v pravoúhlé axonometrii je kruh, jehož poloměrem je poloměr koule. Pro konstrukci (obr. 8.7) je třeba najít střed \(S\) koule a sestrojit příslušnou kružnici se středem v bodě \(S\).