Rovinu zobrazíme pomocí jejích stop. Stopa roviny je průsečnice roviny s průmětnou. Rovina \(\beta\) bude tedy reprezentována půdorysnou stopou \(p^{\beta}\), nárysnou stopou \(n^{\beta}\) a bokorysnou stopou \(m^{\beta}\) (obr. 5.1).

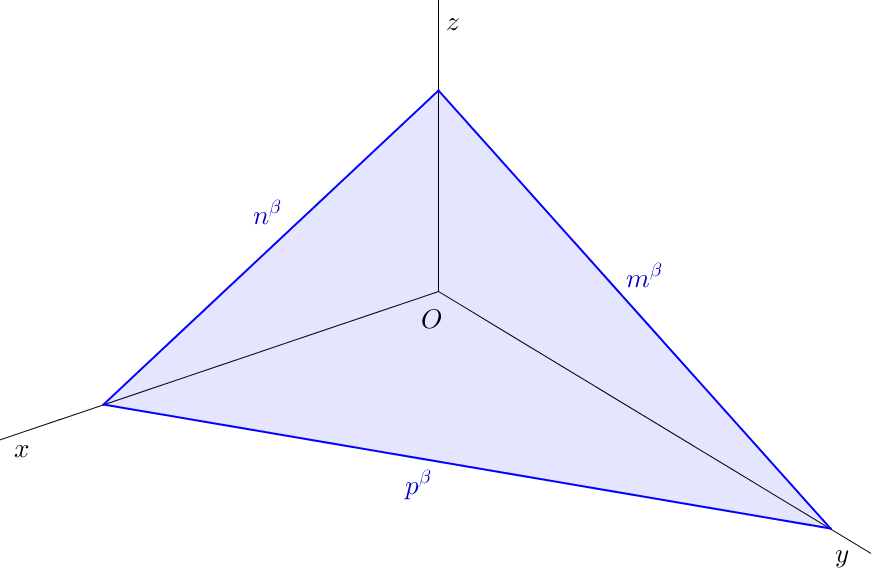
Úloha 19. \(X\)[12-15; 5-19], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Sestrojte stopy roviny \(\varrho = (4;-5;7)\).

Rovina může být zadána třemi nekolineárními body (tj. body, které neleží v jedné přímce), přímkou a bodem (přičemž bod neleží na přímce), nebo dvěma přímkami (rovnoběžnými různými nebo různoběžnými).

Máme-li rovinu zadanou dvěma přímkami, jejími stopami budou spojnice stopníků daných přímek. Spojnicí půdorysných stopníků je půdorysná stopa, spojnicí nárysných stopníků je nárysná stopa, spojnicí bokorysných stopníků je bokorysná stopa.

V případě, že máme rovinu danou bodem a přímkou, vedeme daným bodem rovnoběžku nebo různoběžku s danou přímkou a hledáme stopy roviny zadané dvěma přímkami.

Zadáme-li rovinu pomocí tří bodů (na obr. 5.2 je rovina \(\beta\) zadána body \(K\), \(L\), \(M\)), zadání opět převedeme na dvě přímky (dvě spojnice \(p\), \(q\) libovolně zvolených párů zadaných bodů, popř. spojnice \(p\) dvou bodů a její rovnoběžka \(p'\) nebo různoběžka třetím bodem).

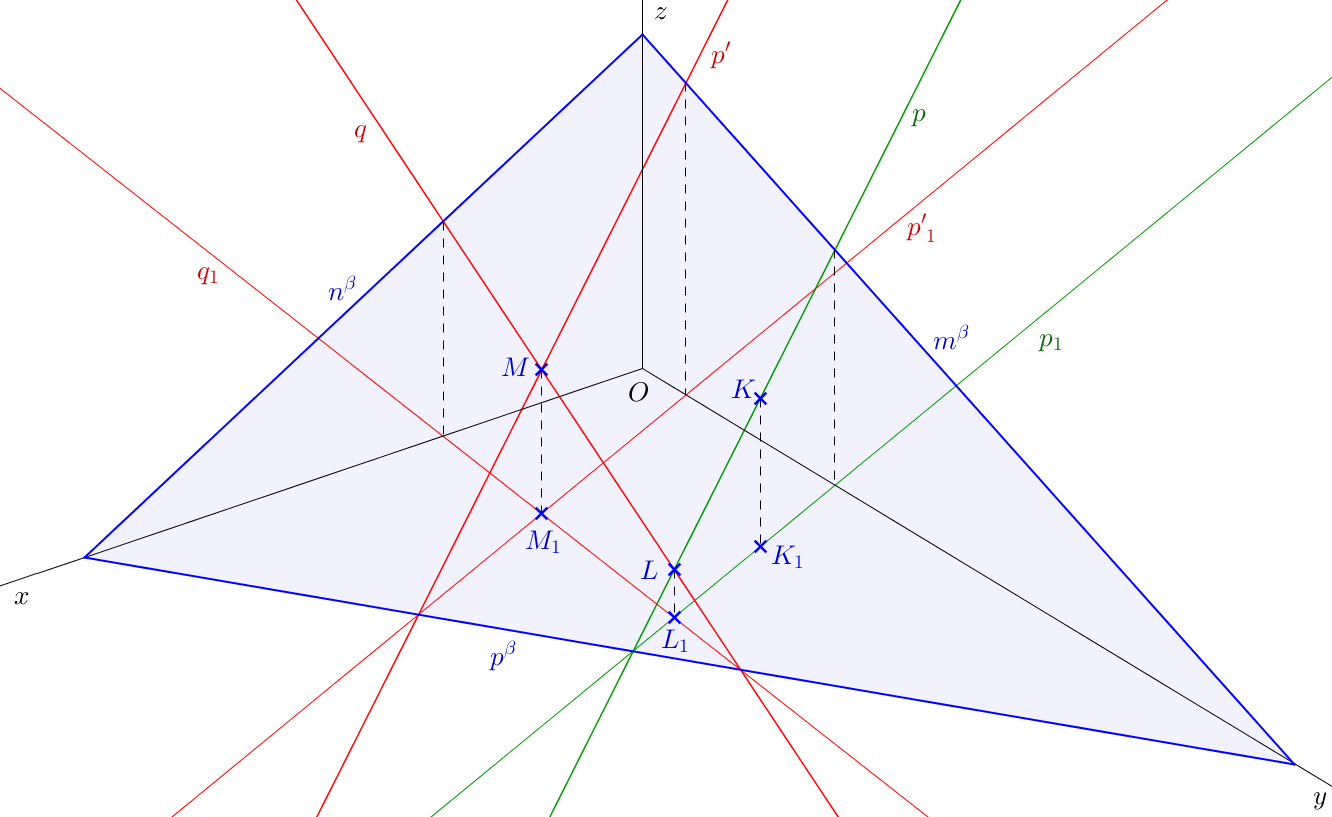
V pravoúhlé axonometrii má rovina navíc axonometrickou stopu \(a^{\beta}\), kterou si ukážeme v kapitole 5.5.

Úloha 20. \(X\)[4-9; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(L=[5,5;3,5;6,5]\), \(M=[0;6;2]\), \(N=[8;0;1]\). Sestrojte stopy roviny \(\rho = LMN\).

Úloha 21. \(X\)[2-7; 7-18], \(\triangle XYZ\): \(|XY|=13\), \(|YZ|=6\), \(|XZ|=12\). Jsou dány body \(A=[4;7;9]\), \(B=[9;1;13]\), \(C=[3;3;10]\). Sestrojte stopy roviny \(\omega = ABC\).