5.1 Přímka a rovina

Vzájemnou polohu přímky \(p\) a roviny \(\beta\) zjistíme pomocí tzv. krycí přímky \(k\), která leží v rovině \(\beta\). Určení vzájemné polohy přímky a roviny si ukážeme na obr. 5.3.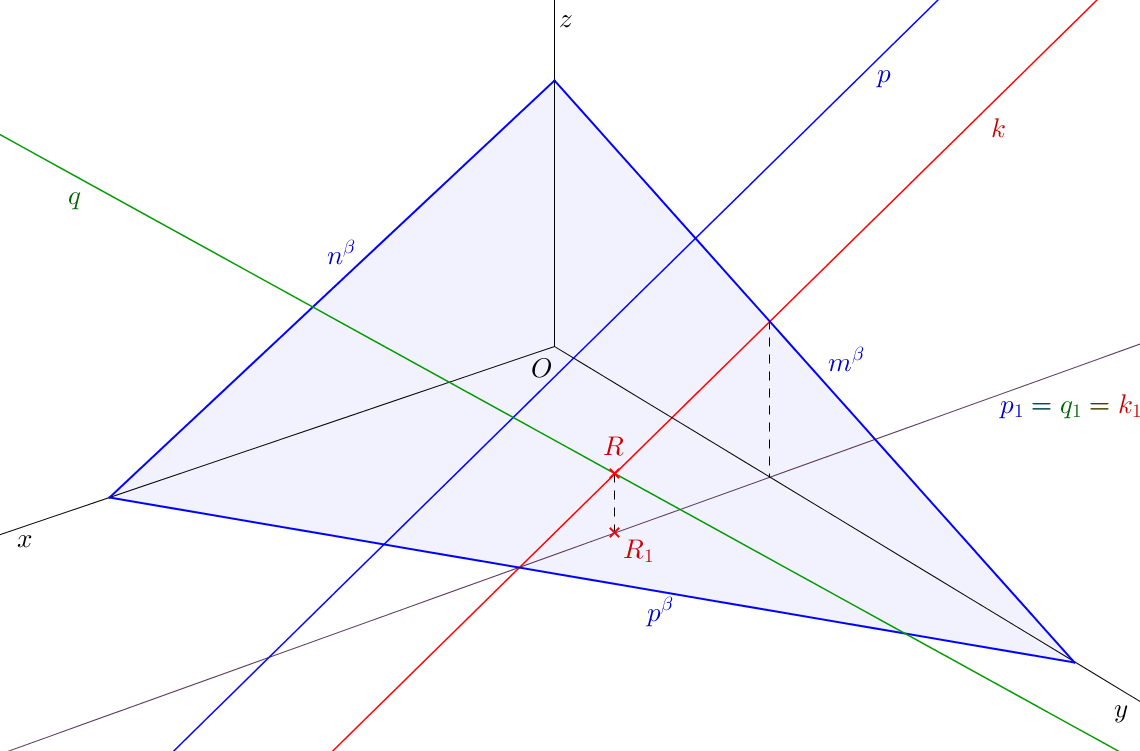

Axonometrický půdorys \(k_{1}\) krycí přímky \(k\) vedeme totožný s axonometrickým půdorysem \(p_{1}\) přímky \(p\). Určíme axonometrický průmět krycí přímky \(k\) (krycí přímka \(k\) leží v rovině \(\beta\), vyneseme tedy po ordinálách její stopníky). Zbývá již pouze porovnat axonometrické průměty krycí přímky \(k\) a přímky \(p\). Jsou-li rovnoběžné, je přímka \(p\) rovnoběžná s rovinou \(\beta\). Mají-li axonometrické průměty přímky \(q\) a k ní takto sestrojené krycí přímky \(k\) společný průsečík \(R\), přímka \(q\) je různoběžná s rovinou \(\beta\) a protíná ji právě v bodě \(R\).

Na obr. 5.3 si můžeme všimnout roviny \(\beta\), přímky \(p\) rovnoběžné s rovinou \(\beta\) a přímky \(q\), která je různoběžná s rovinou \(\beta\). Bod \(R\) je průsečík přímky \(q\) s rovinou \(\beta\).

Podobně můžeme zvolit krycí přímku \(k\), jejíž axonometrický průmět je totožný s axonometrickým průmětem přímky \(p\). Pomocí stopníků určíme axonometrický půdorys \(k_{1}\) přímky \(k\) a porovnáme jej s axonometrickým půdorysem \(p_{1}\) přímky \(p\). Jsou-li průměty \(p_{1}\), \(k_{1}\) rovnoběžné, je i přímka \(p\) rovnoběžná s rovinou \(\beta\). Pokud jsou průměty \(p_{1}\), \(k_{1}\) různoběžné, je přímka \(p\) různoběžná s rovinou \(\beta\). Průsečík \(R_{1}\) přímek \(p_{1}\), \(k_{1}\) je axonometrický půdorys průsečíku přímky \(p\) s rovinou \(\beta\).

Může se stát, že axonometrické průměty přímek \(p\), \(k\) i jejich axonometrické půdorysy budou navzájem totožné (\(p = k \wedge p_{1} = k_{1}\)). Potom přímka \(p\) leží v rovině \(\beta\).

Úloha 22. \(X\)[2-8; 6-20], \(\triangle XYZ\): \(|XY|=10\), \(|YZ|=9\), \(|XZ|=5\). Jsou dány body \(A = [1,5;7;0]\), \(B=[2;2,5;5]\) a rovina \(\varrho =(1,5;1;12)\). Zobrazte průsečík přímky \(p = AB\) s rovinou \(\varrho\).

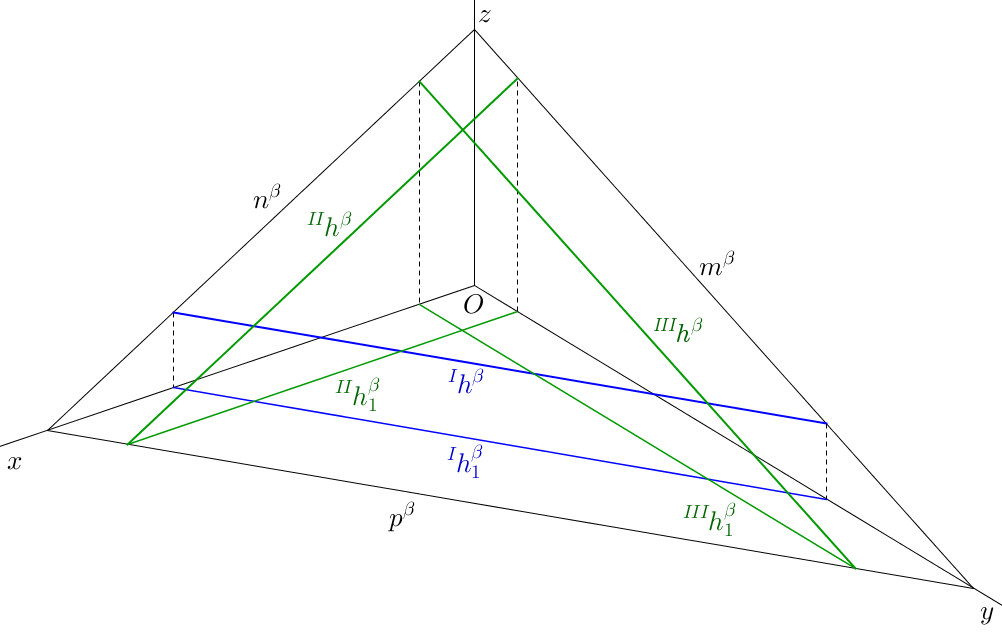
V každé rovině leží nekonečně mnoho přímek. Nyní si ukážeme skupinu speciálních přímek, které se nazývají hlavní přímky. Jde o přímky, které leží v dané rovině a jsou rovnoběžné s pomocnou průmětnou. Rozlišujeme hlavní přímky 1. osnovy, hlavní přímky 2. osnovy a hlavní přímky 3. osnovy. Hlavní přímky 1. osnovy (zvané také horizontální hlavní přímky) jsou rovnoběžné s půdorysnou \(\pi\), hlavní přímky 2. osnovy (též frontální hlavní přímky) jsou rovnoběžné s nárysnou \(\nu\), hlavní přímky 3. osnovy jsou rovnoběžné s bokorysnou \(\mu\). Hlavní přímky 3. osnovy nemají speciální název.

Ukažme si, jak vypadají hlavní přímky v pravoúhlé axonometrii (obr. 5.4): hlavní přímka 1. osnovy \(^Ih^{\beta}\) roviny \(\beta\) je ve skutečnosti rovnoběžná s půdorysnou stopou. Proto jsou oba její průměty (axonometrický \(^Ih^{\beta}\) i půdorysný \(^Ih_{1}^{\beta}\)) rovnoběžné s axonometrickým průmětem stopy \(p^{\beta}\) roviny \(\beta\) (obr. 5.4). Hlavní přímka 2. osnovy \(^{II}h^{\beta}\) je rovnoběžná s nárysnou stopou. Její axonometrický průmět je rovnoběžný s axonometrickým průmětem stopy \(n^{\beta}\) roviny \(\beta\), axonometrický půdorys \(^{II}h_{1}^{\beta}\) je rovnoběžný s axonometrickým průmětem osy \(x\). Podobně potom hlavní přímka 3. osnovy \(^{III}h^{\beta}\) má axonometrický průmět rovnoběžný s axonometrickým průmětem stopy \(m^{\beta}\) roviny \(\beta\), axonometrický půdorys \(^{III}h_{1}^{\beta}\) je rovnoběžný s axonometrickým průmětem osy \(y\).