Strana 5 z 6
5.4 Dvě roviny

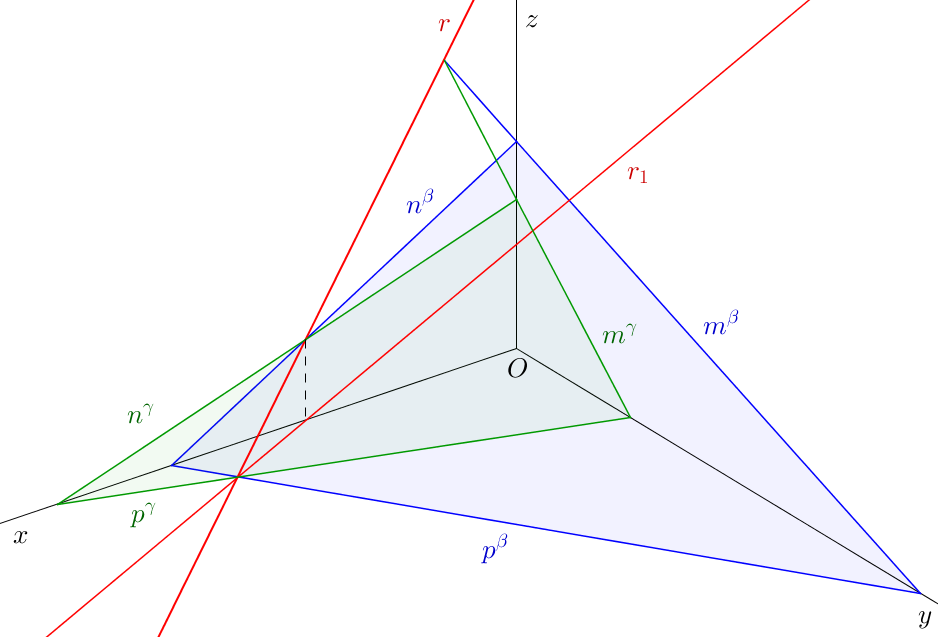
Úloha 23. \(X\)[3-8; 6-20], \(\triangle XYZ\): \(|XY|=10\), \(|YZ|=9\), \(|XZ|=5\). Jsou dány roviny \(\varrho =(1,5;1;12)\), \(\sigma =(8;2;7)\). Zobrazte průsečnici rovin \(\varrho\) a \(\sigma\).


Úloha 23. \(X\)[3-8; 6-20], \(\triangle XYZ\): \(|XY|=10\), \(|YZ|=9\), \(|XZ|=5\). Jsou dány roviny \(\varrho =(1,5;1;12)\), \(\sigma =(8;2;7)\). Zobrazte průsečnici rovin \(\varrho\) a \(\sigma\).