8.1 Hranol
K zobrazení hranolu je třeba zobrazit jeho podstavy a úsečkami správně spojit jednotlivé vrcholy těchto podstav. Musíme tedy umět zobrazit mnohoúhelník (podstavu) v půdorysně a v rovině rovnoběžné s půdorysnou (viz kapitola 6). Na obr. 8.1 vidíme pětiúhelníky \(ABCDE\) a \(A'B'C'D'E'\) jako podstavy kolmého hranolu. Hranol \(ABCDEA'B'C'D'E'\) dokončíme sestrojením úseček \(AA'\), \(BB'\), \(CC'\), \(DD'\), \(EE'\).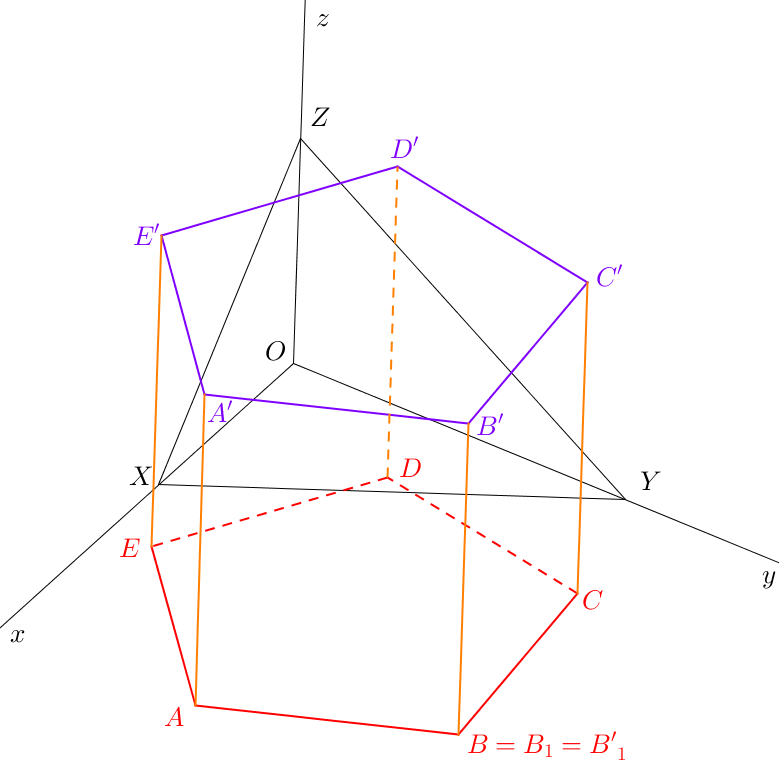
Dále je třeba vyřešit viditelnost hran. Můžeme začít konvexní obálkou všech vrcholů tělesa, která je vždy vidět. Úsečky \(AB\), \(BC\), \(CC'\), \(C'D'\), \(D'E'\), \(E'E\), \(EA\) tedy budou vidět (spojíme plnými čarami). Také víme, že horní podstava bude vidět. Hrany \(E'A'\), \(A'B'\), \(B'C'\) proto rovněž spojíme plnými čarami. Jelikož je hrana \(AA'\) ohraničená dvěma viditelnými vrcholy, bude i tato hrana viditelná. Stejně tak hrana \(BB'\) bude vidět. Zbylé hrany \(CD\), \(DE\), \(DD'\) již vidět nebudou, spojíme je tedy čárkovanými čarami.
Obdobný postup řešení viditelnosti hran lze použít u dalších těles. Při zobrazování dalších těles v tomto textu se viditelností zabývat nebudeme. Nesmíme na ni ale zapomínat.
Úloha 37. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(A=[0;4;3]\), \(S=[0;4;6]\). Sestrojte pravidelný šestiboký hranol \(ABCDEFA'B'C'D'E'F'\), jehož podstava leží v bokorysně. Bod \(S\) je střed podstavy, výška hranolu \(v = 7\). Hranol leží v prvním oktantu. ŘEŠENÍ
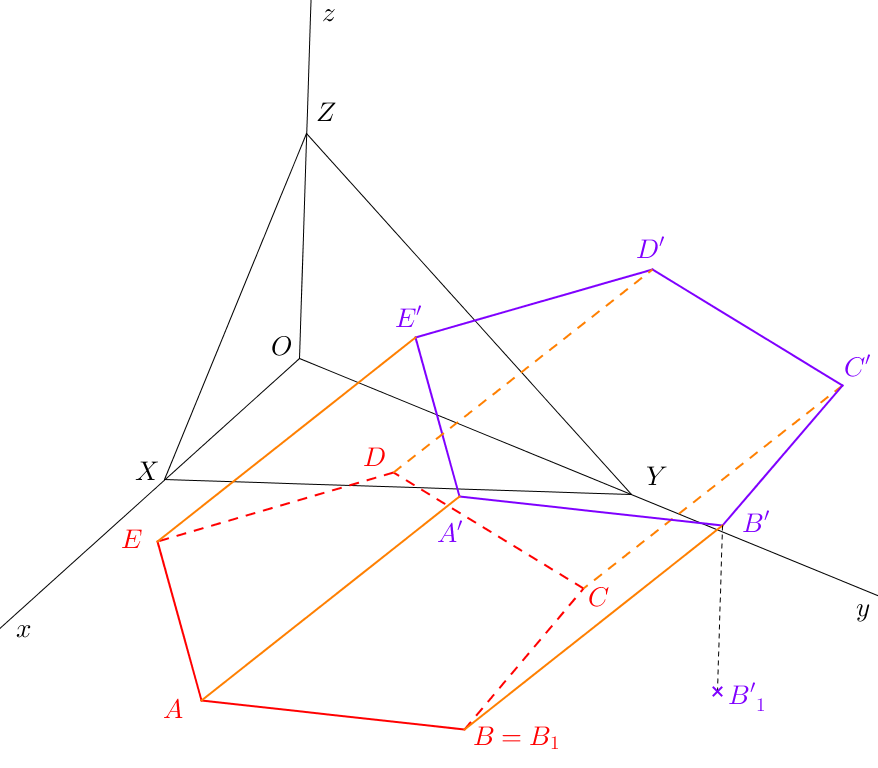
Úloha 38. \(X\)[11; 4-18], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=5\). Jsou dány body \(A=[2;0;5]\), \(B=[9;0;9]\), \(C=[5;0;4]\), \(D=[3,0,4]\), \(E=[1;0;1]\) a délka \(v=5\). Sestrojte kolmý hranol \(ABCDEA'B'C'D'E'\), jehož výška je \(v\). Hranol leží v prvním oktantu.
Úloha 39. \(X\)[4-10; 10-20], \(\triangle XYZ\): \(|XY|=7\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(A=[6;1;0]\), \(B=[8;0;0]\), \(C=[9;8;0]\), \(A'=[7;9;8]\). Sestrojte kosý hranol \(ABCA'B'C'\).
