6.2 Mnohoúhelník v rovině rovnoběžné s půdorysnou

Pro zobrazení mnohoúhelníku \(ABCDE\), který leží v rovině \(\gamma\) rovnoběžné s půdorysnou, zobrazíme nejprve jeho půdorys \(A_{1}B_{1}C_{1}D_{1}E_{1}\), který posuneme ve směru osy \(z\) o \(z\)-ovou souřadnici \(z^\gamma\) roviny \(\gamma\) (viz obr. 6.4), ve které mnohoúhelník leží.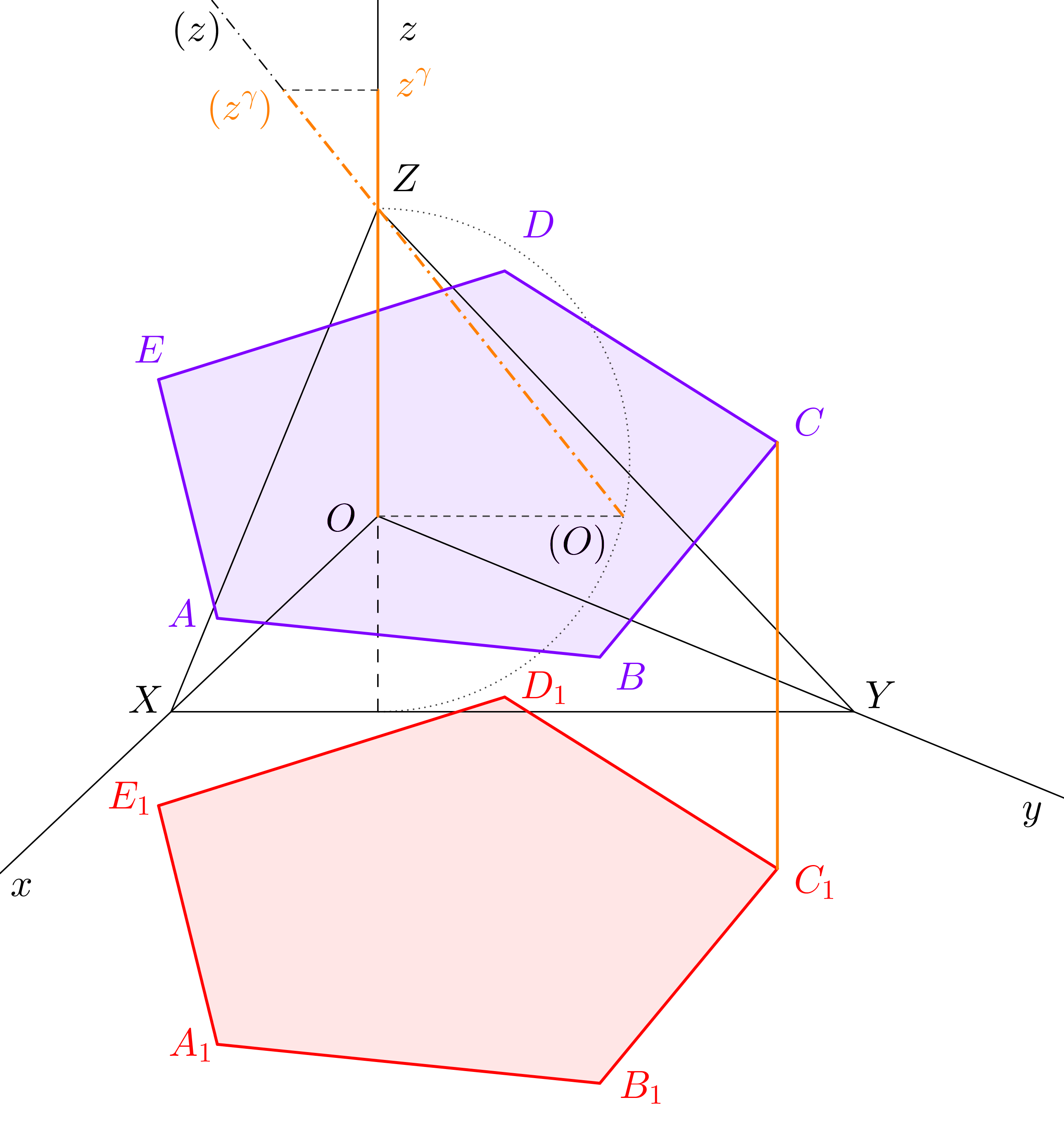

Konstrukce axonometrického půdorysu \(A_{1}B_{1}C_{1}D_{1}E_{1}\) je stejná jako konstrukce mnohoúhelníku ležícího v půdorysně (viz podkapitola 6.1). Pro posunutí mnohoúhelníku do roviny rovnoběžné s půdorysnou potřebujeme vynést \(z\)-ovou souřadnici roviny \(\gamma\). K tomu stačí sklopit promítací rovinu osy \(z\) (viz podkapitola 3.2). Na sklopenou osu naneseme příslušnou \(z\)-ovou souřadnici roviny, ve které mnohoúhelník leží. Souřadnici přeneseme na průmět osy \(z\) a mnohoúhelník posuneme o vektor \(\overrightarrow{Oz^\gamma}\).

Úloha 28. \(X\)[3-10; 8-23], \(\triangle XYZ\): \(|XY|=5\), \(|YZ|=5\), \(|XZ|=3\). Jsou dány body \(A=[4;1;5]\), \(B=[6;7;5]\), \(C=[4;9;5]\), \(D=[0;9;5]\). Sestrojte čtyřúhelník \(ABCD\).

Je-li cílem sestrojit mnohoúhelník ležící v rovině rovnoběžné s nárysnou (nebo bokorysnou), postup je analogický konstrukci mnohoúhelníku ležícího v rovině rovnoběžné s půdorysnou. Nejprve vyneseme jeho axonometrický nárys (bokorys), který následně posuneme ve směru osy \(y\) (\(x\)).