6.1 Vynesení vrcholů z otočené průmětny

Abychom mohli zobrazit mnohoúhelník ležící v půdorysně, musíme nejprve otočit půdorysnu do axonometrické průmětny (viz podkapitola 3.1). Do otočené půdorysny zakreslíme mnohoúhelník ve skutečné velikosti (viz pětiúhelník \(A_{0}B_{0}C_{0}D_{0}E_{0}\) na obr. 6.1).

Otočený mnohoúhelník převedeme zpět do půdorysny tak, že zobrazíme jeho jednotlivé vrcholy, které následně spojíme úsečkami (obr. 6.2). Velmi praktické je užít při zobrazení afinitu (viz obr. 6.3).

Úloha 24. \(X\)[4-8; 9-21], \(\triangle XYZ\): \(|XY|=8\), \(|YZ|=9\), \(|XZ|=7\). Jsou dány body \(A=[4;8;0]\), \(B=[0;4;0]\), \(C=[5;2;0]\), \(D=[2;4;0]\), \(E=[9;6;0]\), \(F=[8;8;0]\), \(G=[1;9;0]\). Sestrojte sedmiúhelník \(ABCDEFG\). ŘEŠENÍ

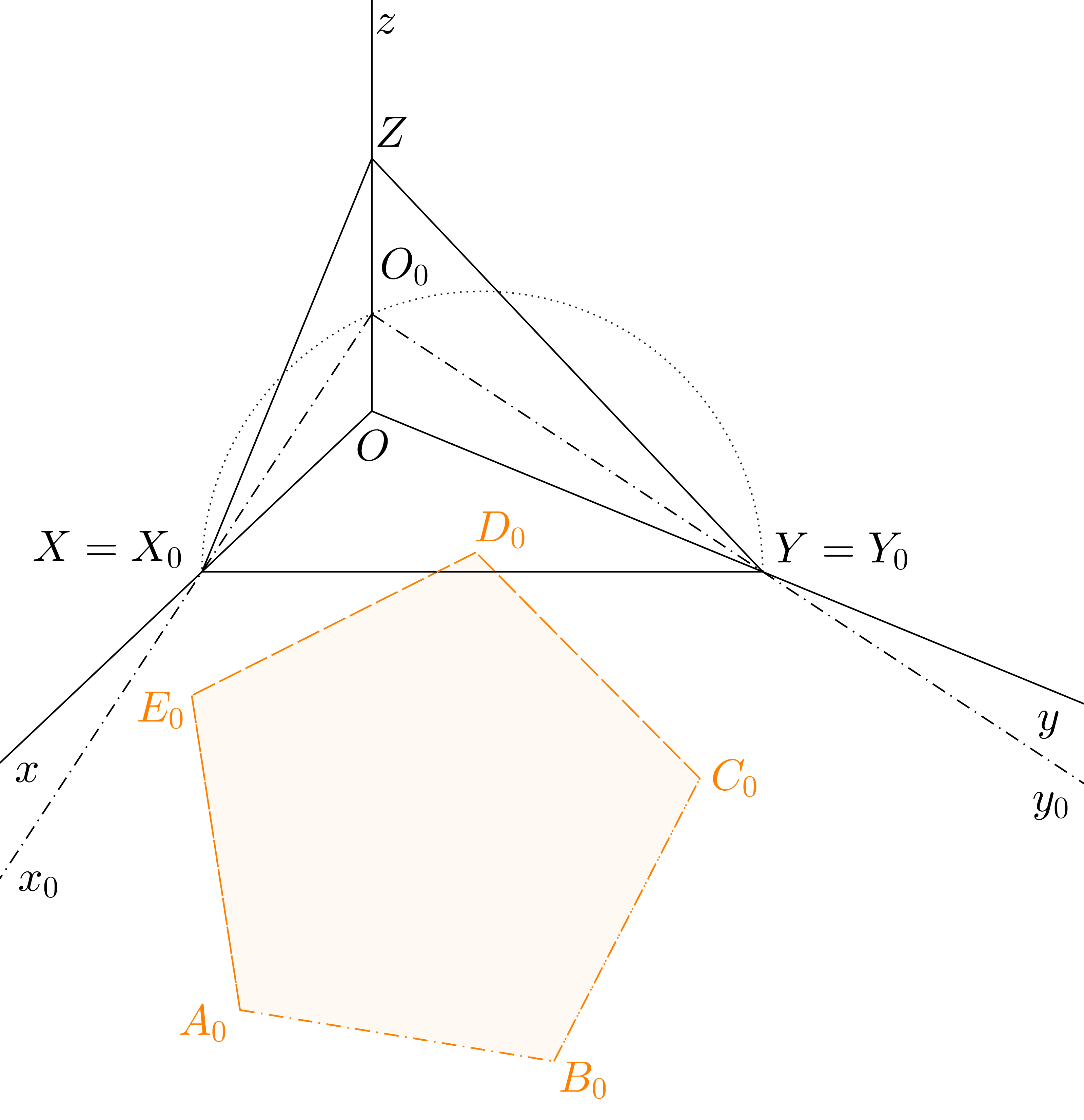
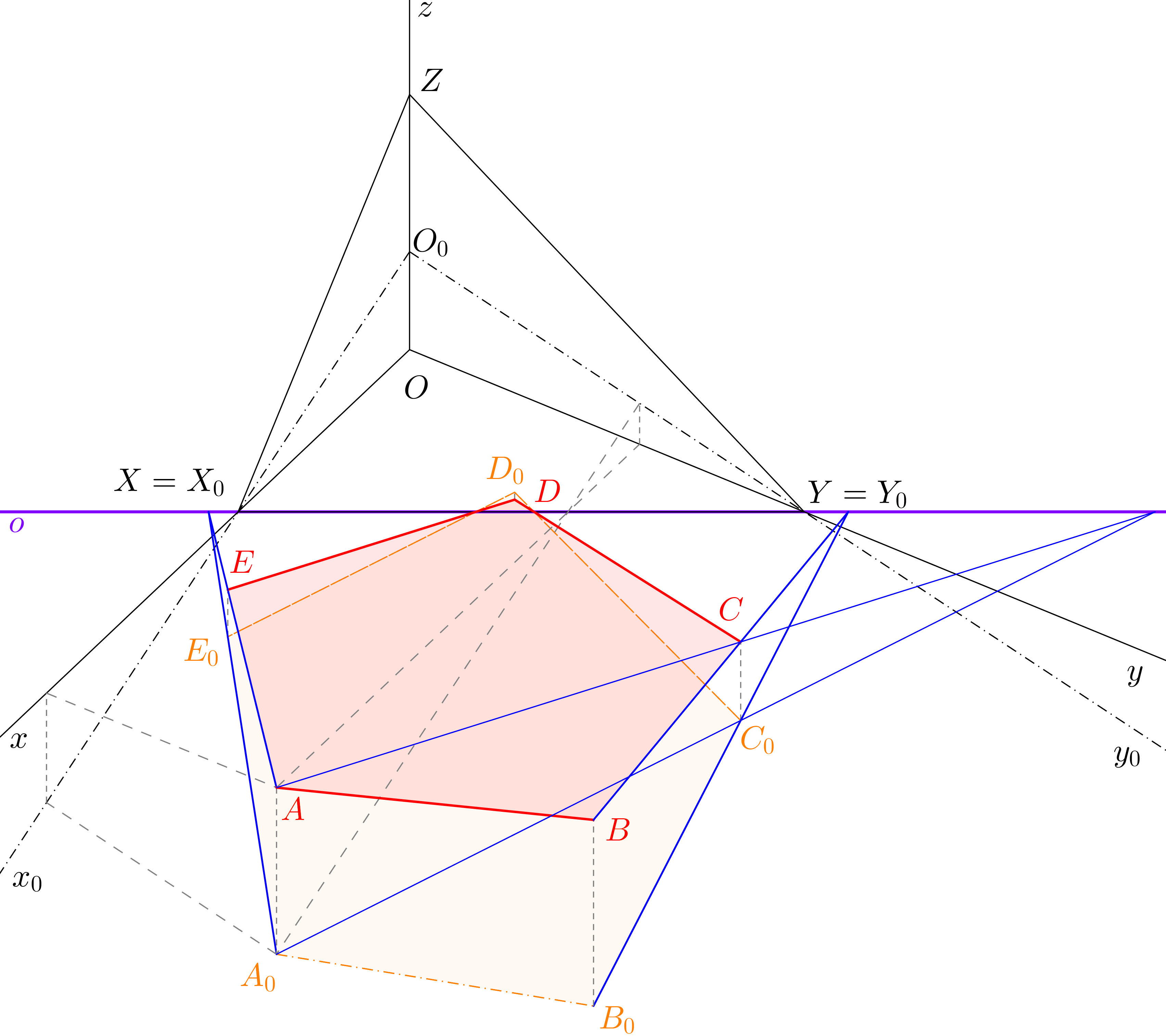
Chceme-li sestrojit mnohoúhelník ležící v nárysně (resp. v bokorysně), namísto půdorysny otočíme nárysnu (bokorysnu). Do otočené nárysny (bokorysny) zobrazíme mnohoúhelník ve skutečné velikosti, který otočíme zpět do axonometrického průmětu nárysny (bokorysny). Osou afinity mezi otočenou nárysnou (bokorysnou) a axonometrickým průmětem nárysny (bokorysny) bude přímka \(XZ\) (\(YZ\)), směrem afinity směr axonometrického průmětu osy \(y\) (\(x\)).

Úloha 25. \(X\)[12-15; 8-23], \(\triangle XYZ\): \(|XY|=5\), \(|YZ|=4\), \(|XZ|=4\). Jsou dány body \(A=[6;0;1]\), \(T=[9;0;4]\). Sestrojte rovnostranný trojúhelník v nárysně s vrcholem \(A\) a těžištěm \(T\).

Úloha 26. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(A=[0;4;3]\), \(S=[0;4;6]\). Sestrojte pravidelný šestiúhelník \(ABCDEF\) se středem \(S\) ležící v bokorysně. ŘEŠENÍ

Úloha 27. \(X\)[5-13; 3-20], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Jsou dány body \(A=[4;0;3]\), \(B=[1;0;6]\). Sestrojte rovnostranný trojúhelník \(ABC\) ležící v nárysně. Zvolte řešení, kdy vrchol \(C\) má největší možné souřadnice. ŘEŠENÍ