3.1 Otočení pomocné průmětny

Do axonometrické průmětny otočíme např. půdorysnu \(\pi\) (obr. 3.2). Stranu \(XY\) axonometrického trojúhelníku vidíme ve skutečné velikosti (\(X = X_{0}\), \(Y = Y_{0}\)). Okolo této strany otočíme rovinu \(\leftrightarrow xy\). Protože body \(X_{0}\), \(Y_{0}\) už známe, stačí otočit počátek \(O\) soustavy souřadnic. Otočený počátek \(O_{0}\) bude ležet v promítací rovině osy \(z\). Zobrazí se tedy na průmět osy \(z\). Zároveň víme, že osy \(x\), \(y\) svírají ve skutečnosti pravý úhel. Otočený počátek tedy musí ležet na Thalétově kružnici nad průměrem \(XY\). Otočené osy \(x_{0}\), \(y_{0}\) jsou určeny body \(O_{0}X_{0}\), resp. \(O_{0}Y_{0}\). Určíme-li nyní na otočených osách \(x_{0}\), \(y_{0}\) jednotky ve skutečné velikosti, jejich axonometrické průměty získáme přenesením na axonometrické průměty os ve směru kolmém k přímce \(XY\).

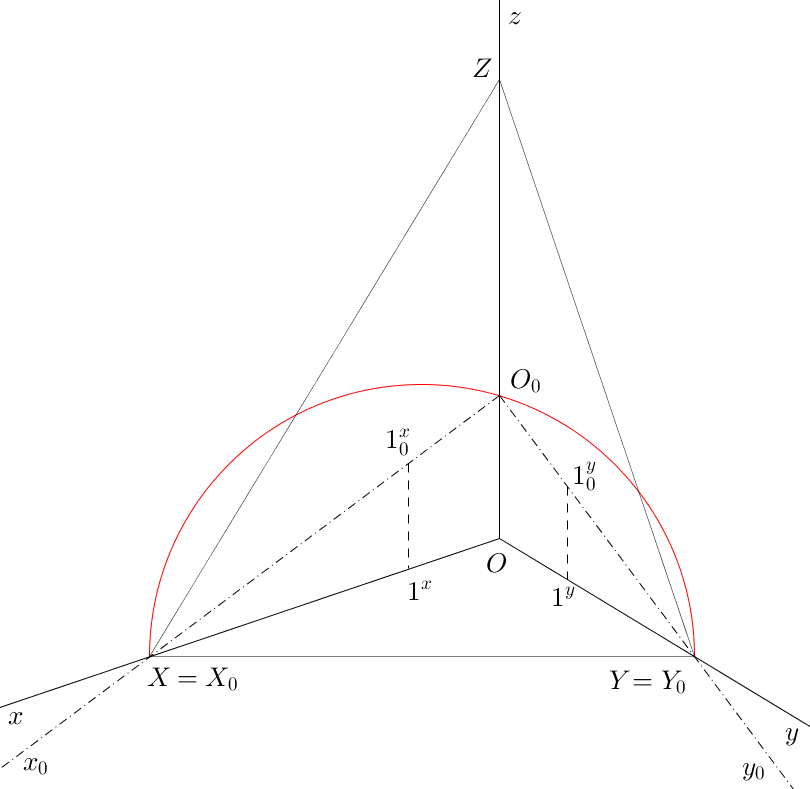
Mezi axonometrickým průmětem půdorysny a jejím otočením platí afinita, jejíž osou je přímka \(XY\), směrem průmět axonometrické osy \(z\) a afinně sdruženými body jsou body \(O\), \(O_{0}\).

Obdobně můžeme do axonometrické průmětny otočit i nárysnu \(\nu\) a bokorysnu \(\mu\).

Úloha 2. \(X\)[3-7; 4-13], \(\triangle XYZ\): \(|XY|=11\), \(|YZ|=17\), \(|XZ|=15\). Určete jednotky na osách \(x\), \(y\). (Otočte půdorysnu do axonometrické průmětny.)

Úloha 3. \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Určete jednotky na osách \(x\), \(y\). (Otočte půdorysnu do axonometrické průmětny.)

Úloha 4. \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Určete jednotky na osách \(x\), \(z\). (Otočte nárysnu do axonometrické průmětny.)

Úloha 5. \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Určete jednotky na osách \(y\), \(z\). (Otočte bokorysnu do axonometrické průmětny.)