3.3 Průmět bodu

K zobrazení bodu v pravoúhlé axonometrii je vhodné kombinovat sklopení promítací roviny osy a otočení pomocné průmětny. Na obr. 3.4 si můžeme všimnout otočení půdorysny \(\pi\) a sklopení promítací roviny osy \(z\). V otočené půdorysně zobrazíme otočený půdorys \( K_{10} \) bodu \(K\) a přeneseme jej na axonometrický půdorys \(K_1\). Na sklopenou osu \(z\) naneseme \(z\)-ovou souřadnici \((z^K)\) bodu \(K\), na axonometrické ose \(z\) určíme axonometrickou \(z\)-ovou souřadnici \(z^K\). Axonometrický průmět \(K\) získáme posunutím axonometrického půdorysu \(K_1\) o vektor \(\overrightarrow{Oz^K}\).

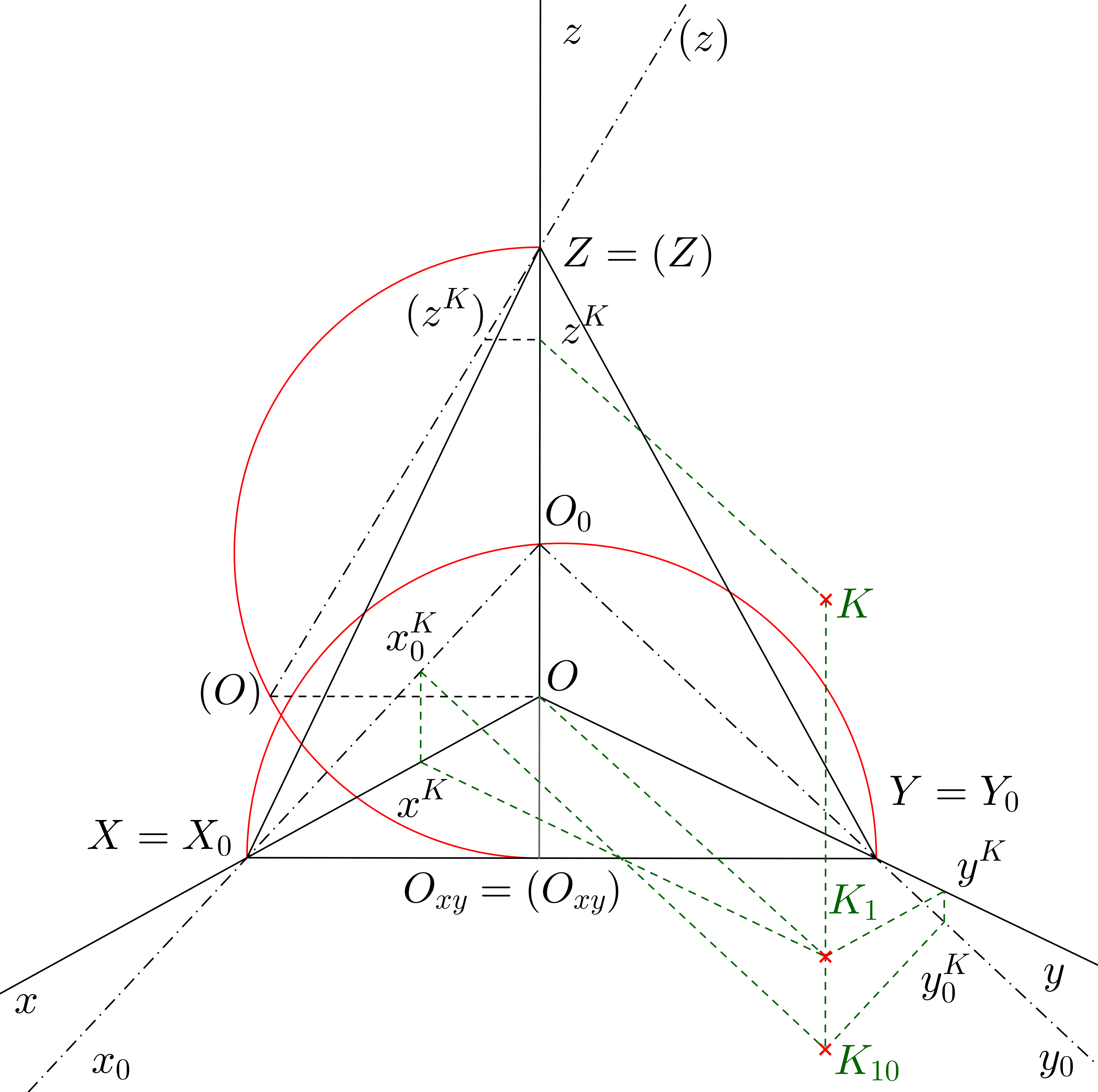
Spojnice axonometrického průmětu bodu s jeho axonometrickým půdorysem (na obr. 3.4 je to přímka \( KK_1\)) se nazývá ordinála.

Chceme-li zobrazit více bodů, je vhodné použít již zmíněnou afinitu mezi otočenou půdorysnou a axonometrickou půdorysnou (porovnání viz obr. 4.2 a 4.3).

Volba této kombinace (otočení půdorysny a sklopení promítací roviny osy \(z\)) je velmi výhodná vzhledem ke skutečnosti, že během konstrukce axonometrického bodu získáme i jeho axonometrický půdorys.

Úloha 10. \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Zobrazte body \(B=[1;0;6]\), \(F=[4;2;5]\).

Úloha 11. \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Zobrazte bod \(A=[0;4;3]\).