Strana 6 z 7
9.5 Řez koule
Pro řez koule ukážeme jenom speciální případy, které jsou postačující, chceme-li získat názorný výkres v pravoúhlé axonometrii. Řezy budeme provádět pouze pomocnými průmětnami a rovinami, které jsou s nimi rovnoběžné. V podkapitole 9.5.1 navíc ukážeme, jak sestrojit řez koule rovinou kolmou k pomocné průmětně.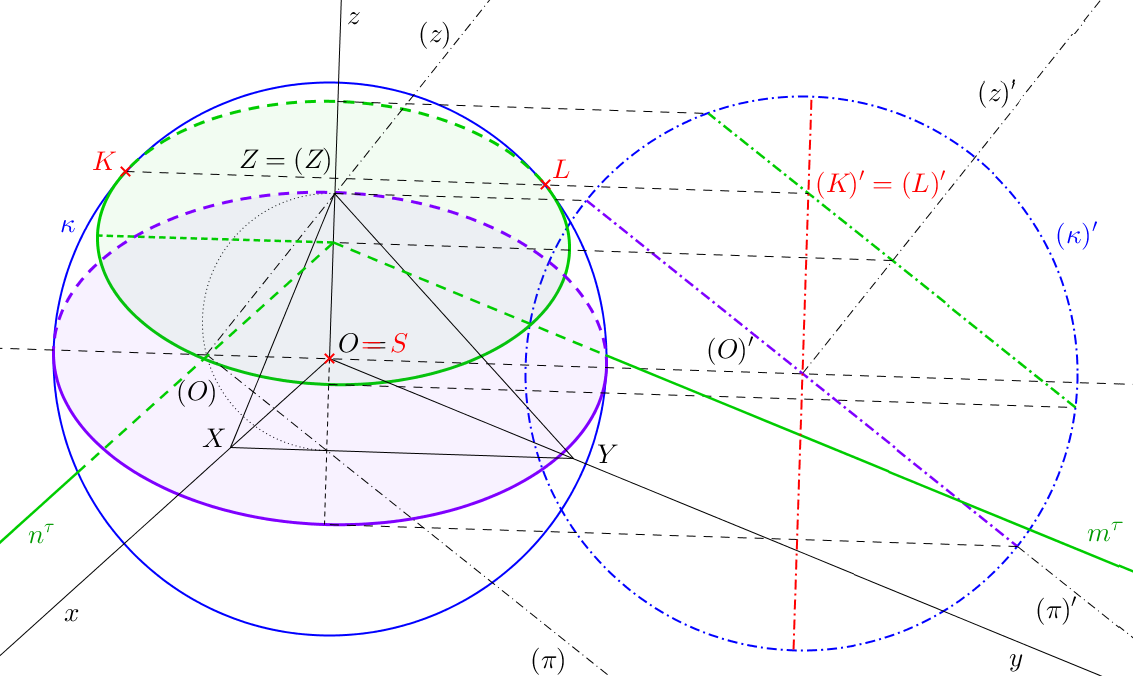
Řezy koule určíme vysunutím sklopené pomocné průmětny. Použijeme promítací rovinu osy \(z\) (viz podkapitola 7.4). Ve vysunuté průmětně zobrazíme průmět koule \((\kappa)'\) a průměty řezů (čerchované úsečky). Hlavní osy axonometrických průmětů řezů jsou kolmé k ose \(z\). Délky hlavních os jsou rovny délkám pomocných průmětů řezů. Vedlejší osy řezu získáme přenesením krajních bodů pomocných průmětů zpět do axonometrie.
K určení viditelnosti řezů potřebujeme nalézt průsečíky řezů s obrysovou kružnicí koule. Ta leží v rovině kolmé k pomocné průmětně, kterou jsme vysunuli. Průmětem obrysové kružnice v pomocné průmětně bude úsečka procházející průmětem středu sféry. Ve vysunutí je úsečka znázorněna červeně. Určíme průsečíky úsečky s průměty řezů a přeneseme je zpět do axonometrie. V případě fialového řezu máme průsečík v bodě \((O)'\). Průsečíkem \((O)'\) povedeme kolmici k axonometrické ose \(z\) a získáme dva průsečíky s obrysem koule. V těchto bodech se řez dotýká obrysu. Mění se zde viditelnost a průmět řezu se dotýká obrysu sféry. Průsečíky zeleného řezu s obrysem sféry nalezneme stejným způsobem. Jsou jimi body \(K\), \(L\).
Zmíněnou červenou úsečkou nyní rozdělme vysunutý průmět koule na dva polokruhy. Směřuje-li vektor \(\overrightarrow{(O)O}\) doprava, části axonometrických řezů vysunuté v pravé polorovině budou vidět. Části v levé polorovině vidět nebudou. Pokud vektor \(\overrightarrow{(O)O}\) směřuje doleva, části řezů v levé polorovině vidět budou, zatímco části ležící v pravé polorovině vidět nebudou.
