Řez tělesa rovinou \(\beta\) je rovinný útvar ležící v rovině \(\beta\) a zároveň v daném tělese. Obecně nemusí mít rovina s tělesem žádné společné body. V tom případě řez nevznikne. Rovina \(\beta\) může mít s tělesem společný jeden bod, úsečku nebo část plochy ohraničenou průnikem roviny s povrchem tělesa, kterou se budeme zabývat v této kapitole. Řezem mnohostěnu tak bude mnohoúhelník, řezy rotačních těles budou plochy ohraničené zpravidla kuželosečkami nebo jejich částmi.

9.1 Řez hranolu

K sestrojení rovinného řezu hranolu je nejjednodušší využít afinity mezi rovinou podstavy hranolu a rovinou řezu.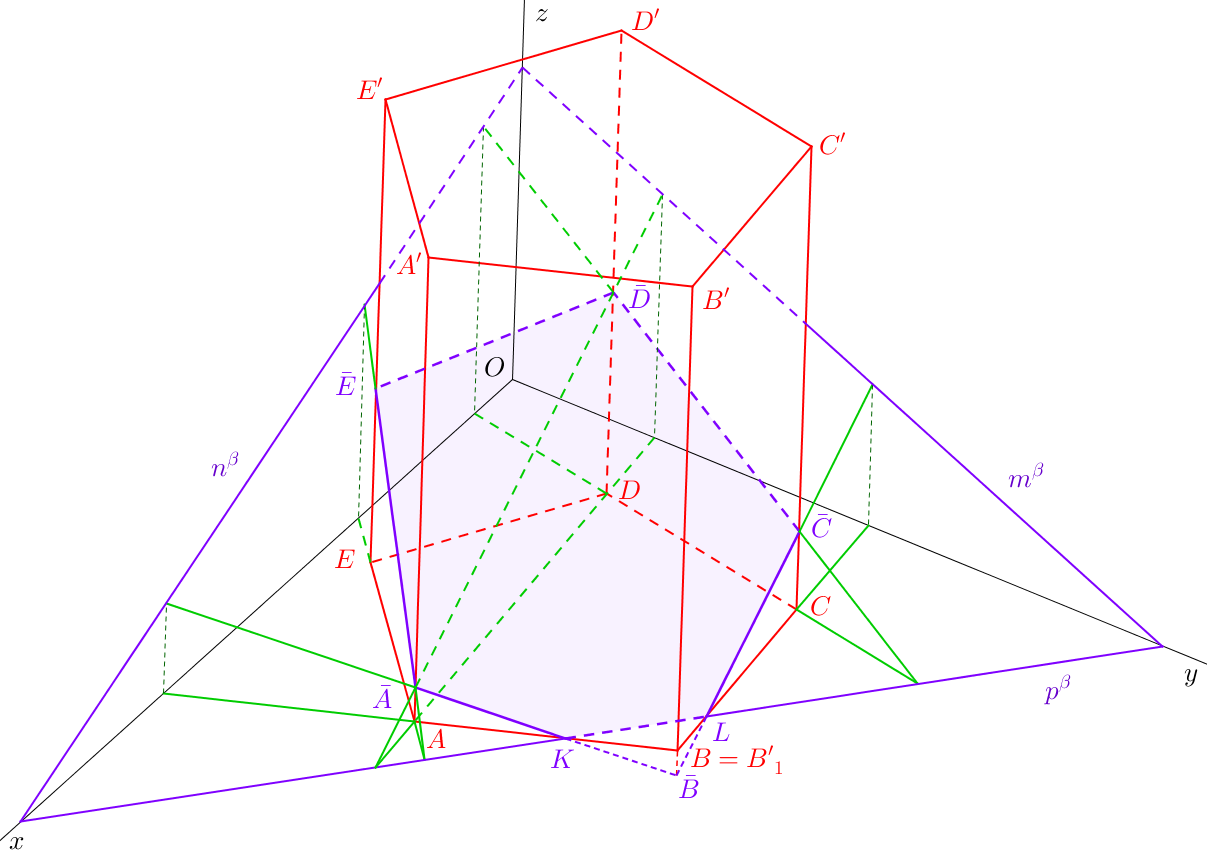

Na obr. 9.1 vidíme kolmý hranol \(ABCDEA'B'C'D'E'\) a rovinu \(\beta\) zadanou svými stopami. Úkolem je sestrojit řez tohoto hranolu rovinou \(\beta\).

Směrem hranolu (a tedy i směrem afinity) je směr bočních hran hranolu, například hrany \(AA'\). Je-li hranol kolmý, afinně sdruženými přímkami k přímkám ležícím v rovině \(\beta\) jsou jejich pravoúhlé průměty do roviny podstavy (na obrázku 9.1 půdorysy - zelené přímky). K určení řezu zvolíme některé z přímek \(AB\), \(BC\), \(CD\), \(DE\), \(AE\), ke kterým pomocí stopníků najdeme přímky afinně sdružené. Průniky roviny \(\beta\) se stěnami řezu tvoří strany řezu. Protíná-li půdorysná stopa roviny řezu podstavu hranolu, tvoří řez rovněž část této stopy ohraničená podstavou (tedy úsečka \(KL\)). Výsledným řezem na obr. 9.1 je šestiúhelník \(\bar{A}KL\bar{C}\bar{D}\bar{E}\).

Stejně jako řešíme viditelnost tělesa, musíme na závěr vyřešit viditelnost řezu. Ohraničuje-li stranu řezu alespoň jedna neviditelná hrana hranolu, je strana řezu neviditelná (na obr. 9.1 se jedná o úsečky \(\bar{C}\bar{D}\) a \(\bar{D}\bar{E}\)). Pro určení viditelnosti ostatních stran řezu si musíme uvědomit, zda strana leží ve stěně hranolu, která je vidět (strany \(\bar{E}\bar{A}\), \(\bar{A}K\), \(L\bar{C}\)), nebo ve stěně, která vidět není (strana \(KL\)).

Stejným způsobem vyřešíme i viditelnost řezů ostatních hranatých těles, proto se jí již dále v textu nezabýváme.

Pamatujme, že rovina řezu může protínat i horní podstavu tělesa. Průsečnici roviny řezu s horní podstavou bychom získali spojením průsečíků lomených čar \(\bar{A}\bar{B}\bar{C}\bar{D}\bar{E}\bar{A}\) a \(A'B'C'D'E'A'\).

Úloha 47. \(X\)[4-10; 7-20], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=6\). Jsou dány body \(A=[6;9;0]\), \(B=[9;3;0]\), \(C=[5;3;0]\), \(D=[5;8;0]\), rovina \(\varrho =(8; \infty ;8)\) a délka \(v=8\). Sestrojte řez kolmého hranolu \(ABCDA'B'C'D'\) rovinou \( \varrho \). Výška hranolu je \(v\).

Úloha 48. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán pravidelný šestiboký hranol \(ABCDEFA'B'C'D'E'F'\) jehož podstava leží v bokorysně. Bod \(A=[0;4;3]\), střed podstavy \(S=[0;4;6]\), výška hranolu \(v = 7\) (viz úloha 37). Sestrojte řez hranolu \(ABCDEFA'B'C'D'E'F'\) rovinou \(\rho = (9;8;14)\). ŘEŠENÍ

Směrem afinity kosého hranolu (obr. 9.2) je rovněž směr bočních hran hranolu. Sdruženými přímkami k přímkám ležícím v rovině řezu však nebudou jejich průměty v rovině podstavy. Než začneme určovat řez hranolu, musíme nejprve najít jeden bod řezu (vyjma samodružných bodů) na libovolné boční hraně.

Na obr. 9.2 je nalezen bod \(\bar{A}\) jako průsečík hrany \(AA'\) s krycí přímkou \(k\) nebo s krycí přímkou \(l\). Nyní již máme zadanou afinitu, s jejíž pomocí řez dokončíme.

Nakonec vyřešíme viditelnost řezu.

Úloha 49. \(X\)[2-6; 3-19], \(\triangle XYZ\): \(|XY|=8\), \(|YZ|=7\), \(|XZ|=8\). Jsou dány body \(A=[8;0;3]\), \(B=[3;0;0]\), \(C=[6;0;6]\), \(A'=[4;6;2]\) a rovina \(\varrho =(8; 9 ;8)\). Sestrojte řez kosého hranolu \(ABCA'B'C'\) rovinou \( \varrho \).

9.2 Řez jehlanu

Řešení rovinného řezu jehlanu nám usnadní užití kolineace mezi rovinou řezu a rovinou podstavy jehlanu. Středem kolineace je hlavní vrchol jehlanu, osou půdorysná stopa roviny řezu.

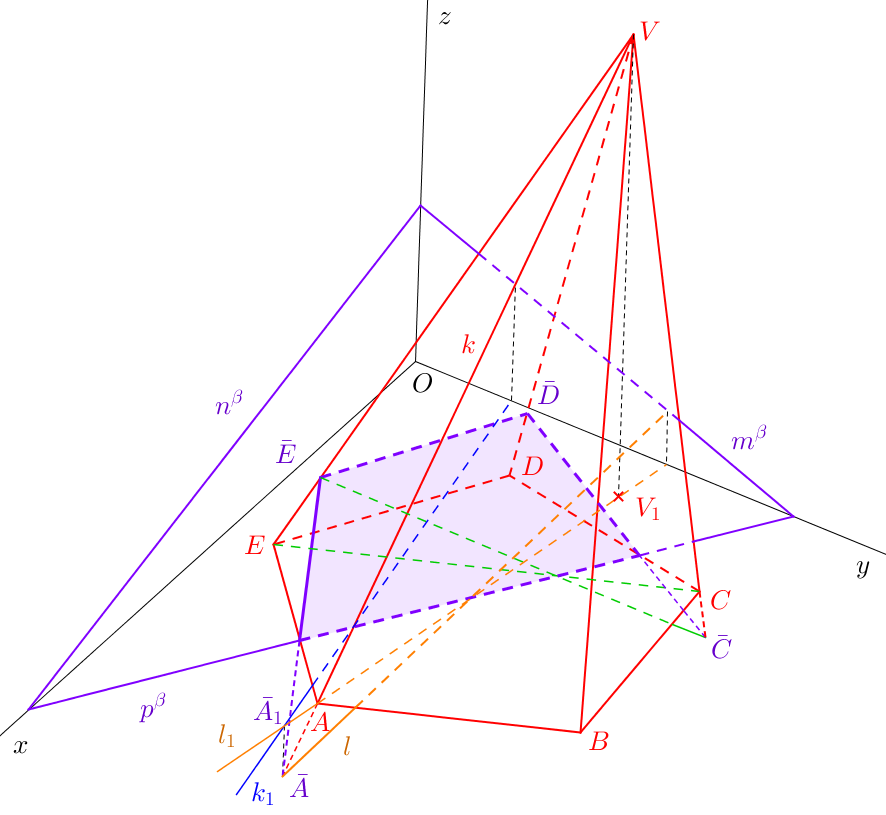
Podobně jako u řezu kosého hranolu, musíme při řešení řezu jehlanu nejprve najít jeden bod řezu (tedy jeden pár bodů sdružených v kolineaci). Na obr. 9.3 hledáme řez jehlanu \(ABCDEV\) rovinou \(\beta\). Můžeme si všimnout nalezení bodu \(\bar{A}\) pomocí krycí přímky \(k\) nebo \(l\). Řez je následně určen pomocí kolineace. Viditelnost řezu určíme stejně jako u řezů hranolů.

Úloha 50. \(X\)[5-13; 3-20], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Je dán pravidelný trojboký jehlan \(ABCV\) s podstavou v nárysně. Výška jehlanu \(v = 7\), body \(A=[4;0;3]\), \(B=[1;0;6]\) (viz úloha 40). Sestrojte řez jehlanu rovinou \(\rho = (4;-5;7)\). ŘEŠENÍ

Úloha 51. \(X\)[7-12; 8-19], \(\triangle XYZ\): \(|XY|=5\), \(|YZ|=4\), \(|XZ|=6\). Jsou dány body \(A=[5;5;0]\), \(B=[8;0;0]\), \(C=[3;1;0]\), \(V=[1;7;9]\) a  rovina \(\varrho =(8; \infty ;8)\). Sestrojte řez jehlanu \(ABCV\) rovinou \( \varrho \).

Řez komolého jehlanu může ovlivnit jeho druhá podstava. Stejně jako při řešení řezů hranolů musíme sledovat, zda rovina řezu druhou podstavu protíná, či nikoliv.

9.3 Řez rotačního válce

Je-li rovina řezu směrovou rovinou rotačního válce, řezem je obdélník. Pokud je rovina řezu rovnoběžná s rovinou podstavy (tj. v našem případě s půdorysnou), řezem je kruh (průmětem řezu je plocha ohraničená elipsou). V ostatních případech je řezem válce plocha ohraničená elipsou, nebo její část. Elipsu určíme jednoznačně, najdeme-li její sdružené průměry. Sdružené průměry řezu získáme jako afinně sdružené úsečky ke kolmým průměrům podstavy.

K nalezení řezu rotačního válce obecnou rovinou nám pomůže afinita mezi rovinou řezu a rovinou podstavy válce.

Na obr. 9.4 je vyřešen řez válce rovinou \(\beta\), která je určena svými stopami. Zeleně je vyznačena dvojice afinně sdružených průměrů podstavy a řezu (zvolili jsme průměry, které jsou v podstavě rovnoběžné s osami \(x\), \(y\), tedy ve skutečnosti kolmé). Lze také použít přímo hlavní a vedlejší osu průmětu podstavy (hlavní osa je na obrázku modře).

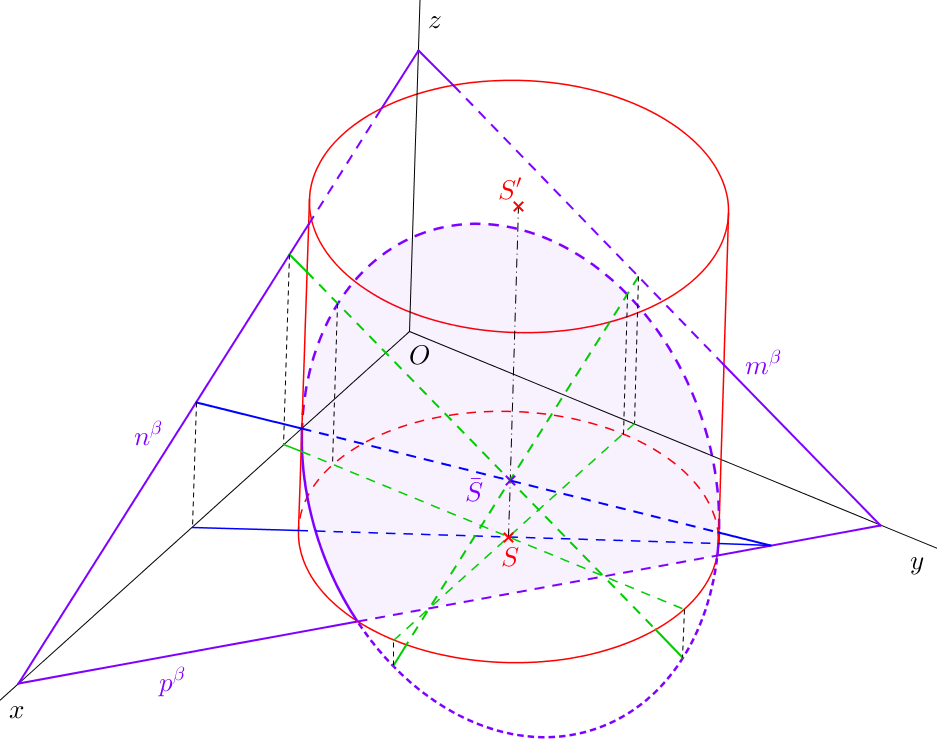
Viditelnost řezu se mění na obrysových površkách válce. Část řezu, která je afinně sdružená s viditelnou částí podstavy, je vidět, část sdružená s neviditelnou částí podstavy vidět není. Protíná-li rovina řezu podstavu, vzniklá část řezu v podstavě je viditelná, je-li viditelná podstava. Pokud rovina řezu protíná podstavu, která je neviditelná, průsečnice roviny s touto podstavou je neviditelná.

Úloha 52. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán rotační válec, jehož podstava se středem \(S=[8;8;0]\) a poloměrem \(r=3\) leží v půdorysně, výška válce je \(v=7\) (viz úloha 43). Sestrojte řez válce rovinou \(\omega = (10; \infty ;9)\). ŘEŠENÍ

Úloha 53. \(X\)[4-10; 14-22], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=6\), \(|XZ|=3\). Je dán bod \(S=[7;2;0]\), délky \(r=3\), \(v=6\) a rovina \(\varrho =(10; \infty ;6)\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v půdorysně. Výška válce je \(v\). Sestrojte řez válce rovinou \(\varrho\).

9.4 Řez rotačního kužele

Určení řezu rotačního kužele je náročnější, než je tomu u válce. Řezem není vždy elipsa nebo kružnice. Může vzniknout i parabola nebo hyperbola (v případě vrcholové roviny trojúhelník). Parabolický a hyperbolický řez můžeme vynést bod po bodu pomocí kolineace mezi rovinou řezu a rovinou podstavy.

K eliptickému řezu umíme najít sdružené průměry. Musíme být ale obezřetní, protože se postup zásadně liší od určování řezu válce. Na obr. 9.5 je kužel a rovina \(\beta\). Jeden průměr hledané elipsy najdeme na spádové přímce \(s^\beta\) roviny \(\beta\) různoběžné s osou kužele (axonometrický půdorys spádové přímky přeneseme z otočené půdorysny jako kolmici ke stopě roviny \(\beta\), axonometrický průmět získáme vynesením stopníků přímky \(s^\beta\)). Průnik přímky \(s^\beta\) s kuželem je jedním průměrem řezu. Nyní určíme střed \(\hat{S}\) tohoto průměru. Střed \(\hat{S}\) neleží na ose kužele.

Sdružený průměr leží na hlavní přímce \(h^\beta\) roviny \(\beta\). Vedeme tedy středem \(\hat{S}\) přímku \(h^\beta\) rovnoběžnou se stopou \(p^\beta\). Touto přímkou proložíme vrcholovou rovinu a určíme její průsečíky s kružnicí, která ohraničuje podstavu kužele. Průsečíky spojíme přímkami s vrcholem \(V\), tzv. povrchovými přímkami kužele. Na povrchových přímkách leží krajní body průměru.

Viditelnost řezu určujeme stejně jako u válce. Body řezu, které jsou v kolineaci sdružené s viditelnými body podstavy, jsou vidět a naopak. Leží-li část řezu v podstavě, závisí viditelnost této části řezu na viditelnosti podstavy. (Je-li podstava neviditelná, část řezu v podstavě je také neviditelná a naopak.)

Úloha 54. \(X\)[3-9; 2-18], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán rotační kužel s podstavou v půdorysně. Střed podstavy \(S=[0;0;0]\), poloměr podstavy \(r=3\), výška kužele \(v=10\) (viz úloha 45). Sestrojte řez kužele rovinou \(\psi=(5; \infty; 6)\). ŘEŠENÍ

9.5 Řez koule

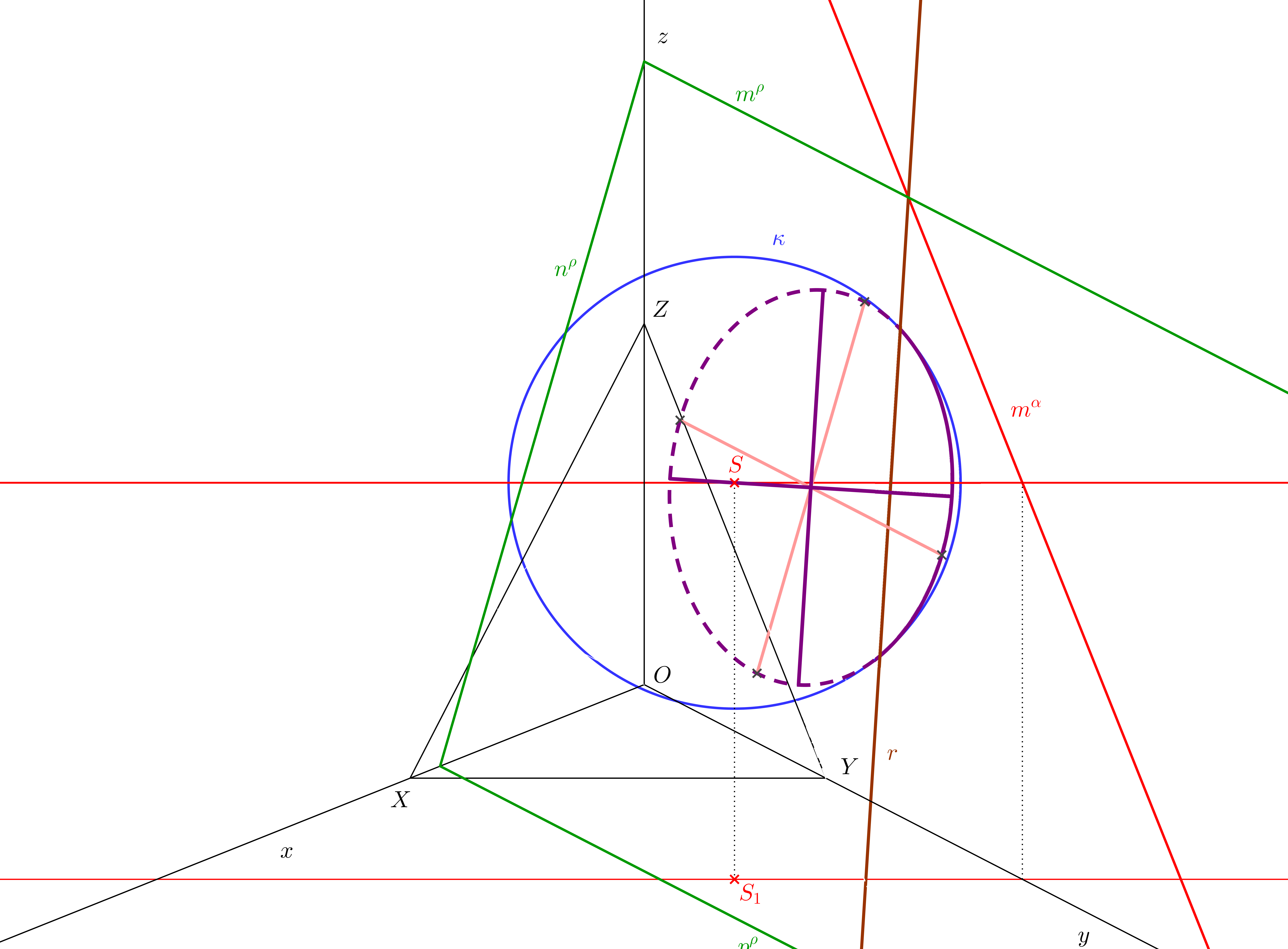
Pro řez koule ukážeme jenom speciální případy, které jsou postačující, chceme-li získat názorný výkres v pravoúhlé axonometrii. Řezy budeme provádět pouze pomocnými průmětnami a rovinami, které jsou s nimi rovnoběžné. V podkapitole 9.5.1 navíc ukážeme, jak sestrojit řez koule rovinou kolmou k pomocné průmětně.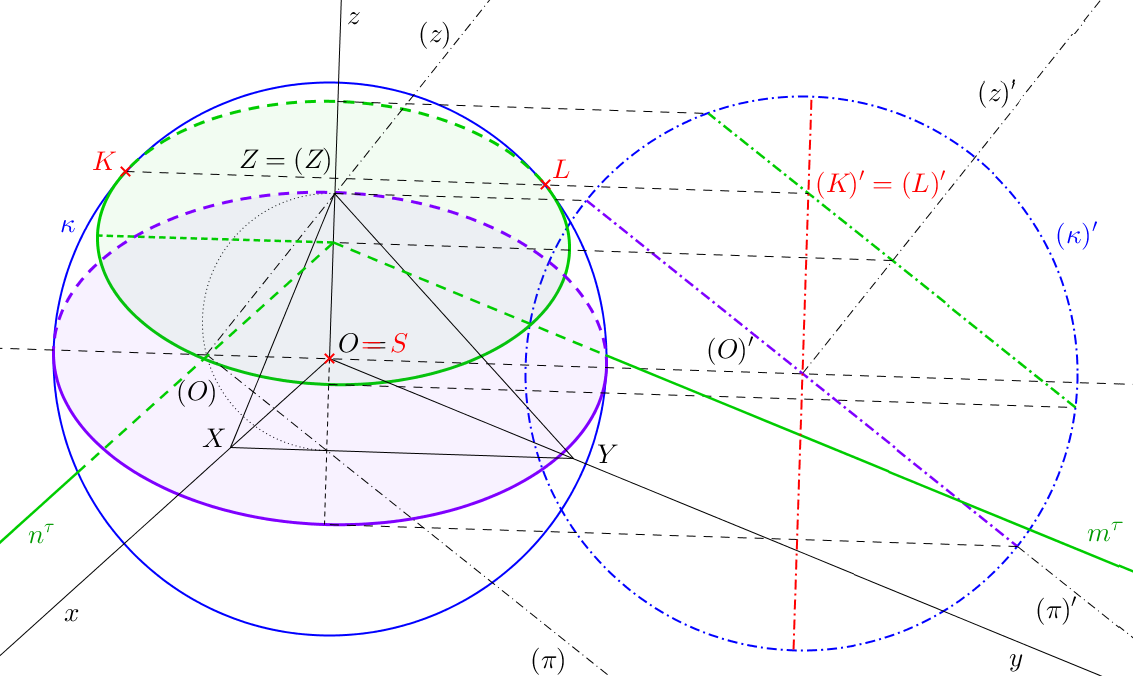

Koulí \(\kappa\) se středem \(S\) v počátku soustavy souřadnic \(O\) (obr. 9.6) vedeme řez půdorysnou (fialově) a řez rovinou \(\tau\), která je s půdorysnou rovnoběžná (zeleně). Řezem koule je vždy kruh, jehož průmětem bude část roviny ohraničená elipsou.

Řezy koule určíme vysunutím sklopené pomocné průmětny. Použijeme promítací rovinu osy \(z\) (viz podkapitola 7.4). Ve vysunuté průmětně zobrazíme průmět koule \((\kappa)'\) a průměty řezů (čerchované úsečky). Hlavní osy axonometrických průmětů řezů jsou kolmé k ose \(z\). Délky hlavních os jsou rovny délkám pomocných průmětů řezů. Vedlejší osy řezu získáme přenesením krajních bodů pomocných průmětů zpět do axonometrie.

K určení viditelnosti řezů potřebujeme nalézt průsečíky řezů s obrysovou kružnicí koule. Ta leží v rovině kolmé k pomocné průmětně, kterou jsme vysunuli. Průmětem obrysové kružnice v pomocné průmětně bude úsečka procházející průmětem středu sféry. Ve vysunutí je úsečka znázorněna červeně. Určíme průsečíky úsečky s průměty řezů a přeneseme je zpět do axonometrie. V případě fialového řezu máme průsečík v bodě \((O)'\). Průsečíkem \((O)'\) povedeme kolmici k axonometrické ose \(z\) a získáme dva průsečíky s obrysem koule. V těchto bodech se řez dotýká obrysu. Mění se zde viditelnost a průmět řezu se dotýká obrysu sféry. Průsečíky zeleného řezu s obrysem sféry nalezneme stejným způsobem. Jsou jimi body \(K\), \(L\).

Zmíněnou červenou úsečkou nyní rozdělme vysunutý průmět koule na dva polokruhy. Směřuje-li vektor \(\overrightarrow{(O)O}\) doprava, části axonometrických řezů vysunuté v pravé polorovině budou vidět. Části v levé polorovině vidět nebudou. Pokud vektor \(\overrightarrow{(O)O}\) směřuje doleva, části řezů v levé polorovině vidět budou, zatímco části ležící v pravé polorovině vidět nebudou.

9.5.1 Řez koule rovinou kolmou k pomocné průmětně

V této podkapitole vyřešíme řez koule rovinou, která je kolmá k pomocné průmětně, ale není rovnoběžná s jinou pomocnou průmětnou (obr. 9.7). Protože je konstrukce poměrně náročná, budeme ji ilustrovat více obrázky.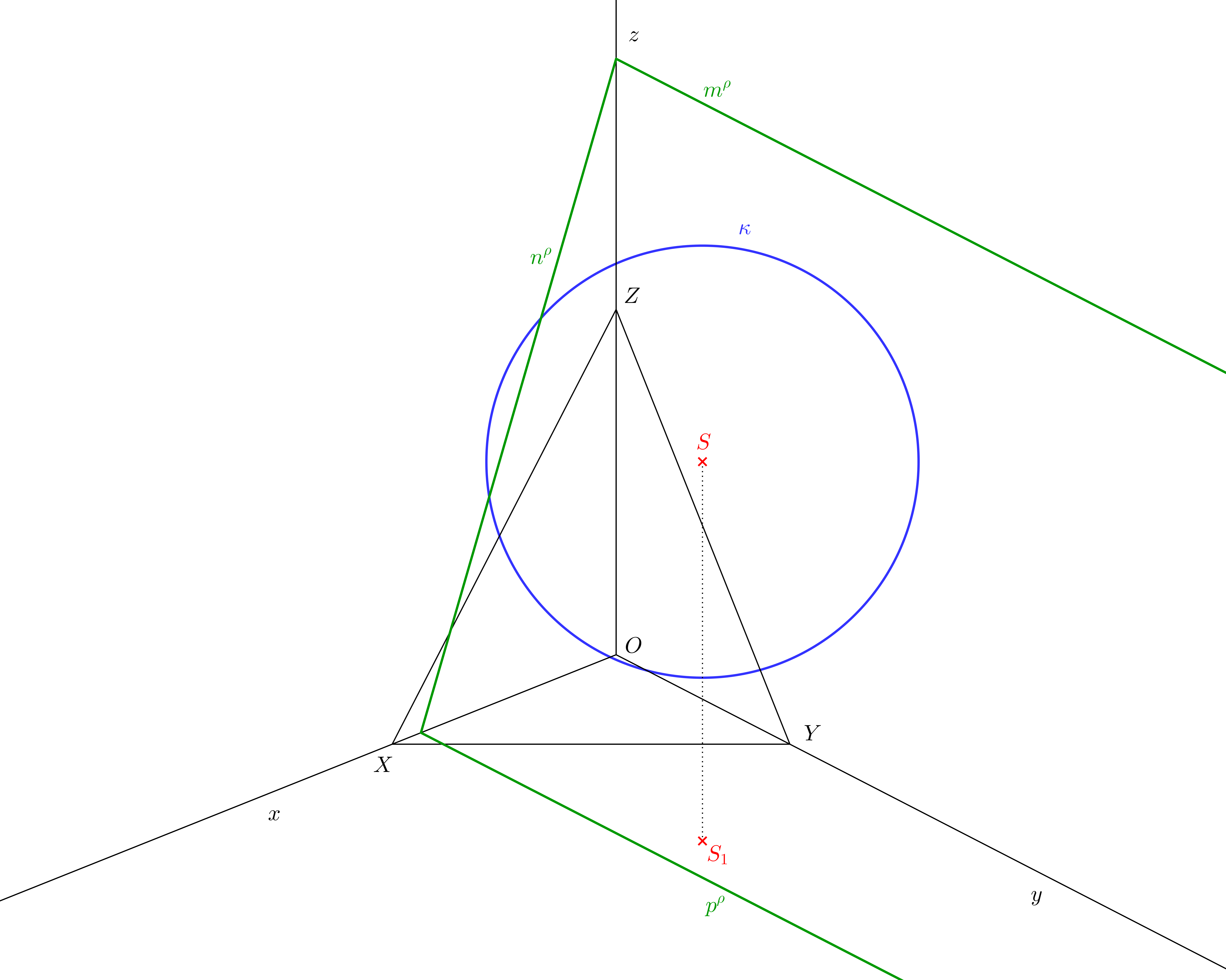

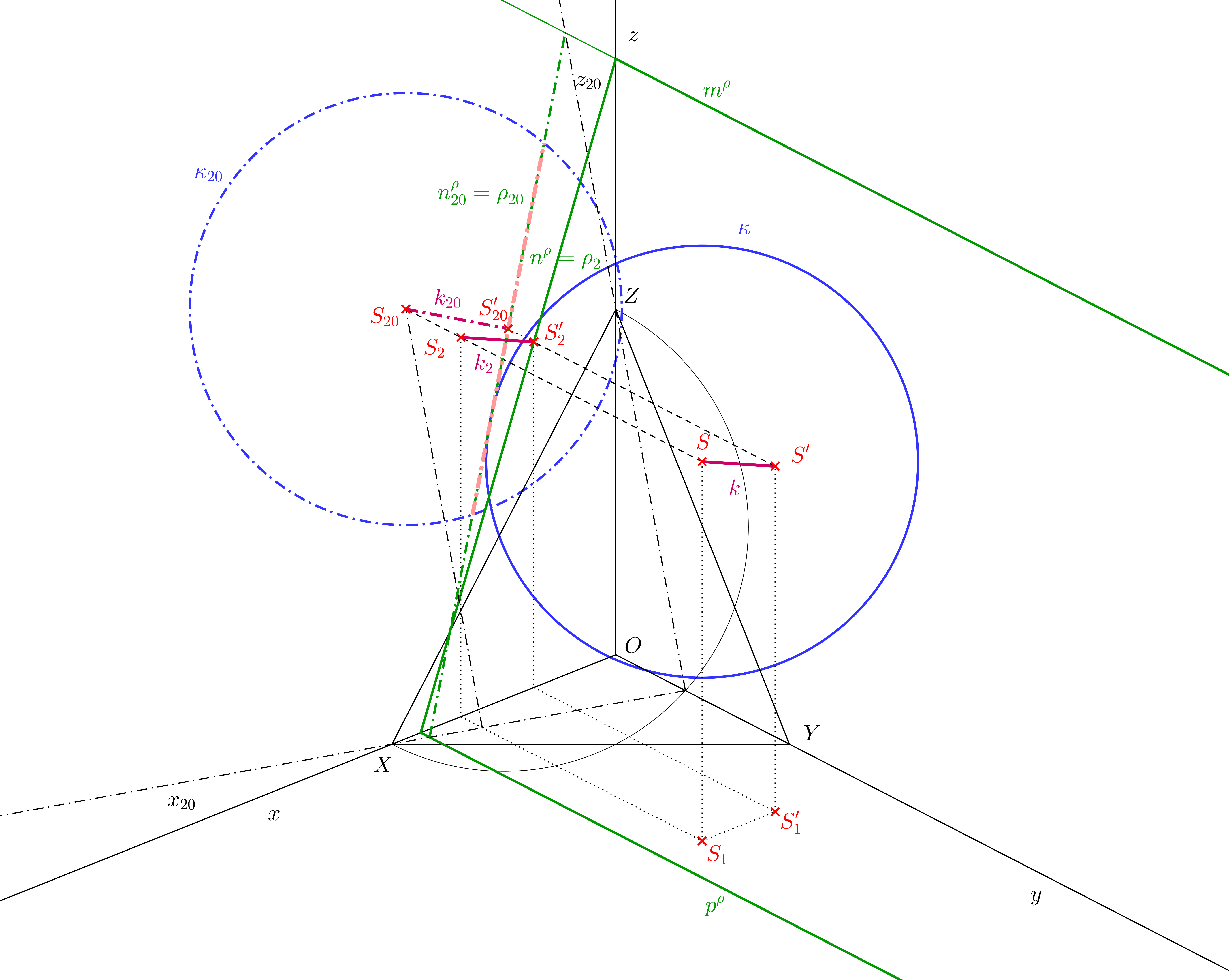
Úlohu vyřešíme pomocí průmětu situace do pomocné průmětny, která je kolmá k rovině řezu. V tomto pomocném průmětu získáme všechny údaje potřebné k vyřešení úlohy.

Zadaná rovina \(\rho\) je kolmá k nárysně. Jejím nárysem tak bude nárysná stopa \(n^\rho\) (\(\rho_2 = n^\rho\)), nárysem řezu bude úsečka. Otočíme nárysnu do axonometrické průmětny a určíme nárys situace v otočení (obr. 9.8).

Střed řezu \(S'\) najdeme na kolmici k rovině řezu \(k\) vedené středem sféry \(S\) (obr. 9.9). Konstrukci kolmice \(k\) provedeme v otočení: přímka \(k_{20}\) je kolmá k přímce \(n^\rho_{20}\), pata kolmice \(S'_{20}\) leží na přímce \(n^\rho_{20} = \rho_{20}\).

Bod \(S'_{20}\) leží na přímce \(n^\rho_{20}\), tedy bod \(S'_2\) bude ležet na přímce \(n^\rho_2 = n^\rho\). Nárys kolmice \(k_2\) prochází body \(S_2\), \(S'_2\). Kolmice \(k\) je rovnoběžná s nárysnou. Je tedy rovnoběžná se svým nárysem \(k_2\). Axonometrický průmět přímky \(k\) je tedy rovnoběžný s axonometrickým průmětem přímky \(k_2\). Proto bod \(S'\) najdeme na přímce \(k\), která je rovnoběžná s přímkou \(k_2\).

Dále rýsujeme kružnici v rovině \(\rho\) se středem \(S'\). Poloměr kružnice vidíme v otočení ve skutečné velikosti. Na obr. 9.10 je zobrazen řez v axonometrii - fialově jsou vyznačeny hlavní a vedlejší osa axonometrického průměru elipsy, růžově průměr rovnoběžný s nárysnou a průměr kolmý k nárysně (tedy sdružené průměry elipsy).

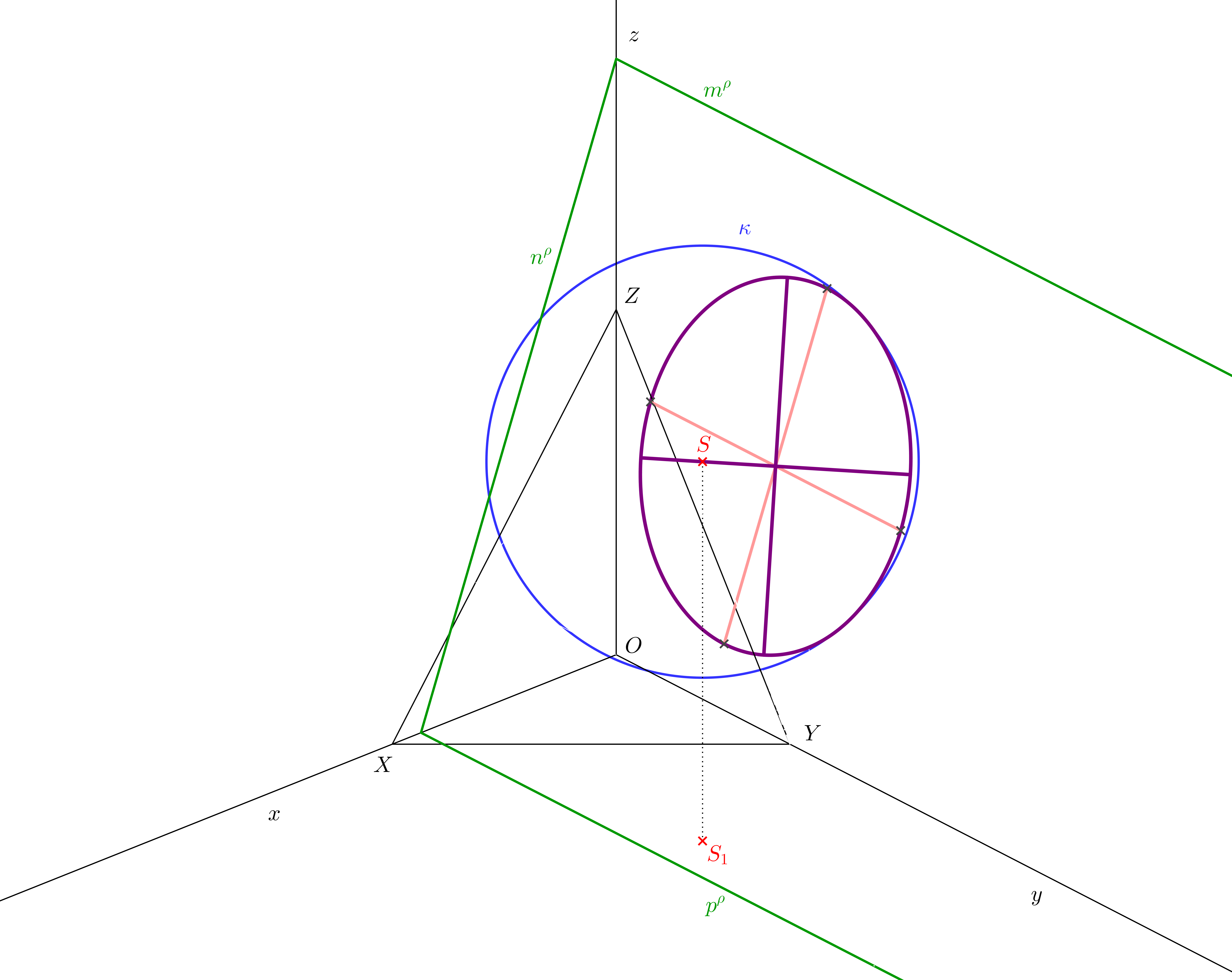
Viditelnost řezu se mění na obrysu koule. Obrys koule leží v rovině rovnoběžné s axonometrickou průmětnou, která prochází středem koule. Tuto rovinu najdeme a určíme její průsečnici s rovinou řezu koule. Na průsečnici leží body na obrysu, ve kterých se mění viditelnost.

Na obr. 9.11 je bokorysná roviny \(\alpha\), ve které leží obrys koule. Stopy nalezneme pomocí bokorysného stopníku přímky, která prochází středem \(S\) a je rovnoběžná s přímkou \(XY\). (Stopy roviny \(\alpha\) jsou rovnoběžné se stranami axonometrického trojúhelníku, tj. se stopami axonometrické průmětny.) Průsečnice \(r\) rovin \(\alpha\), \(\rho\) dělí řez na viditelnou a neviditelnou část.