9.2 Řez jehlanu

Řešení rovinného řezu jehlanu nám usnadní užití kolineace mezi rovinou řezu a rovinou podstavy jehlanu. Středem kolineace je hlavní vrchol jehlanu, osou půdorysná stopa roviny řezu.

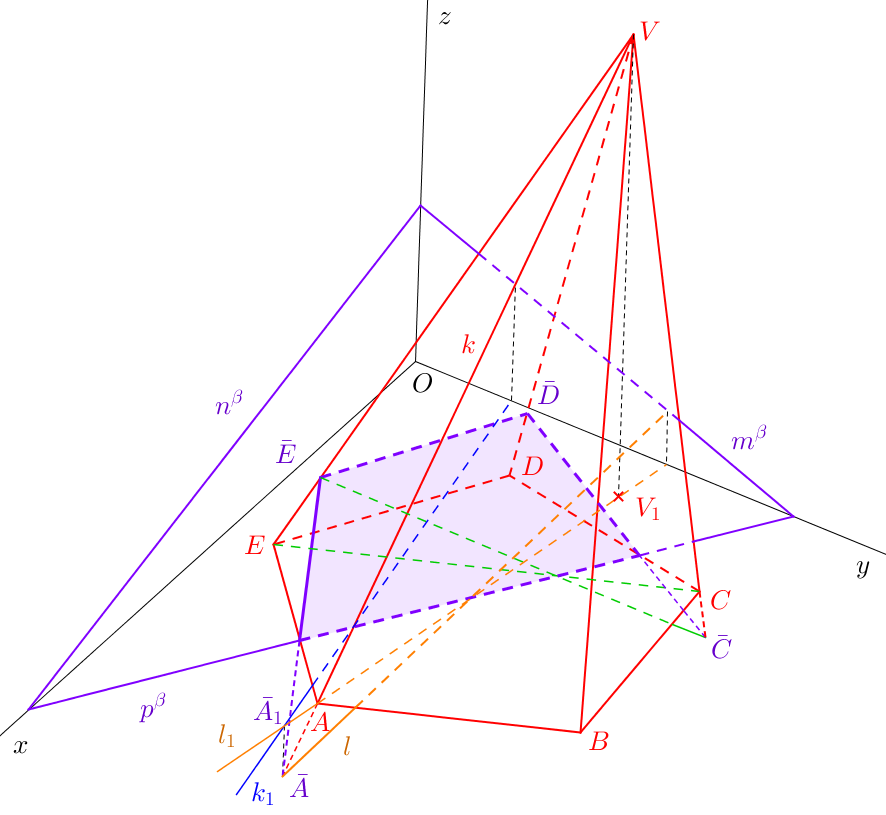
Podobně jako u řezu kosého hranolu, musíme při řešení řezu jehlanu nejprve najít jeden bod řezu (tedy jeden pár bodů sdružených v kolineaci). Na obr. 9.3 hledáme řez jehlanu $ABCDEV$ rovinou $\beta$. Můžeme si všimnout nalezení bodu $\bar{A}$ pomocí krycí přímky $k$ nebo $l$. Řez je následně určen pomocí kolineace. Viditelnost řezu určíme stejně jako u řezů hranolů.

Úloha 50. $X$[5-13; 3-20], $\triangle XYZ$: $|XY|=6$, $|YZ|=7$, $|XZ|=5$. Je dán pravidelný trojboký jehlan $ABCV$ s podstavou v nárysně. Výška jehlanu $v = 7$, body $A=[4;0;3]$, $B=[1;0;6]$ (viz úloha 40). Sestrojte řez jehlanu rovinou $\rho = (4;-5;7)$. ŘEŠENÍ

Úloha 51. $X$[7-12; 8-19], $\triangle XYZ$: $|XY|=5$, $|YZ|=4$, $|XZ|=6$. Jsou dány body $A=[5;5;0]$, $B=[8;0;0]$, $C=[3;1;0]$, $V=[1;7;9]$ a  rovina $\varrho =(8; \infty ;8)$. Sestrojte řez jehlanu $ABCV$ rovinou $\varrho$.

Řez komolého jehlanu může ovlivnit jeho druhá podstava. Stejně jako při řešení řezů hranolů musíme sledovat, zda rovina řezu druhou podstavu protíná, či nikoliv.