9.3 Řez rotačního válce

Je-li rovina řezu směrovou rovinou rotačního válce, řezem je obdélník. Pokud je rovina řezu rovnoběžná s rovinou podstavy (tj. v našem případě s půdorysnou), řezem je kruh (průmětem řezu je plocha ohraničená elipsou). V ostatních případech je řezem válce plocha ohraničená elipsou, nebo její část. Elipsu určíme jednoznačně, najdeme-li její sdružené průměry. Sdružené průměry řezu získáme jako afinně sdružené úsečky ke kolmým průměrům podstavy.

K nalezení řezu rotačního válce obecnou rovinou nám pomůže afinita mezi rovinou řezu a rovinou podstavy válce.

Na obr. 9.4 je vyřešen řez válce rovinou \(\beta\), která je určena svými stopami. Zeleně je vyznačena dvojice afinně sdružených průměrů podstavy a řezu (zvolili jsme průměry, které jsou v podstavě rovnoběžné s osami \(x\), \(y\), tedy ve skutečnosti kolmé). Lze také použít přímo hlavní a vedlejší osu průmětu podstavy (hlavní osa je na obrázku modře).

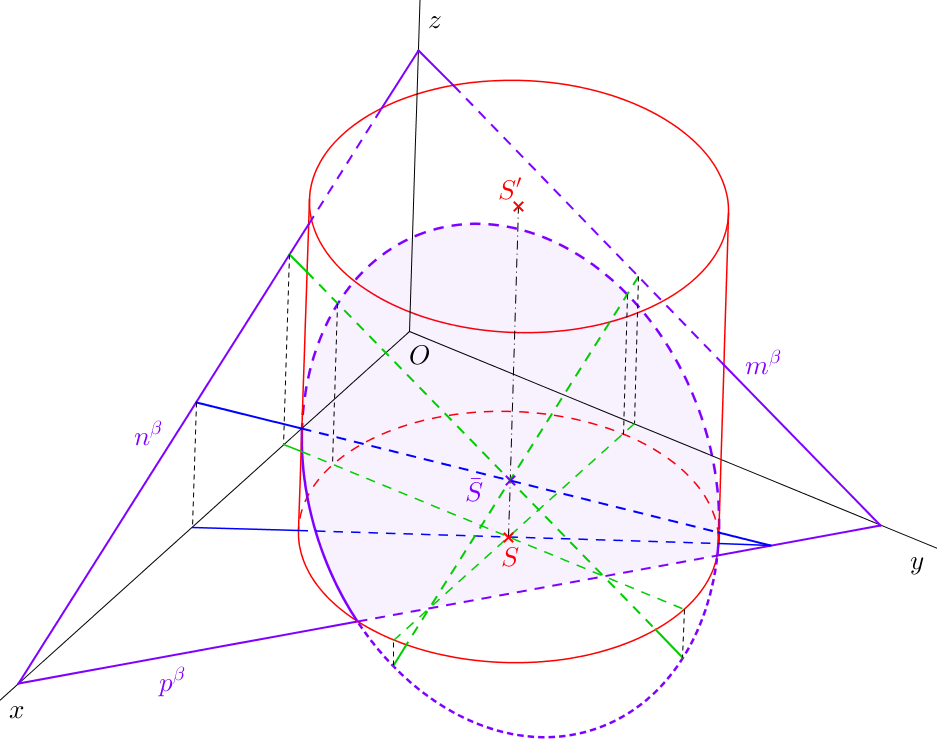
Viditelnost řezu se mění na obrysových površkách válce. Část řezu, která je afinně sdružená s viditelnou částí podstavy, je vidět, část sdružená s neviditelnou částí podstavy vidět není. Protíná-li rovina řezu podstavu, vzniklá část řezu v podstavě je viditelná, je-li viditelná podstava. Pokud rovina řezu protíná podstavu, která je neviditelná, průsečnice roviny s touto podstavou je neviditelná.

Úloha 52. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán rotační válec, jehož podstava se středem \(S=[8;8;0]\) a poloměrem \(r=3\) leží v půdorysně, výška válce je \(v=7\) (viz úloha 43). Sestrojte řez válce rovinou \(\omega = (10; \infty ;9)\). ŘEŠENÍ

Úloha 53. \(X\)[4-10; 14-22], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=6\), \(|XZ|=3\). Je dán bod \(S=[7;2;0]\), délky \(r=3\), \(v=6\) a rovina \(\varrho =(10; \infty ;6)\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v půdorysně. Výška válce je \(v\). Sestrojte řez válce rovinou \(\varrho\).