9.1 Řez hranolu

K sestrojení rovinného řezu hranolu je nejjednodušší využít afinity mezi rovinou podstavy hranolu a rovinou řezu.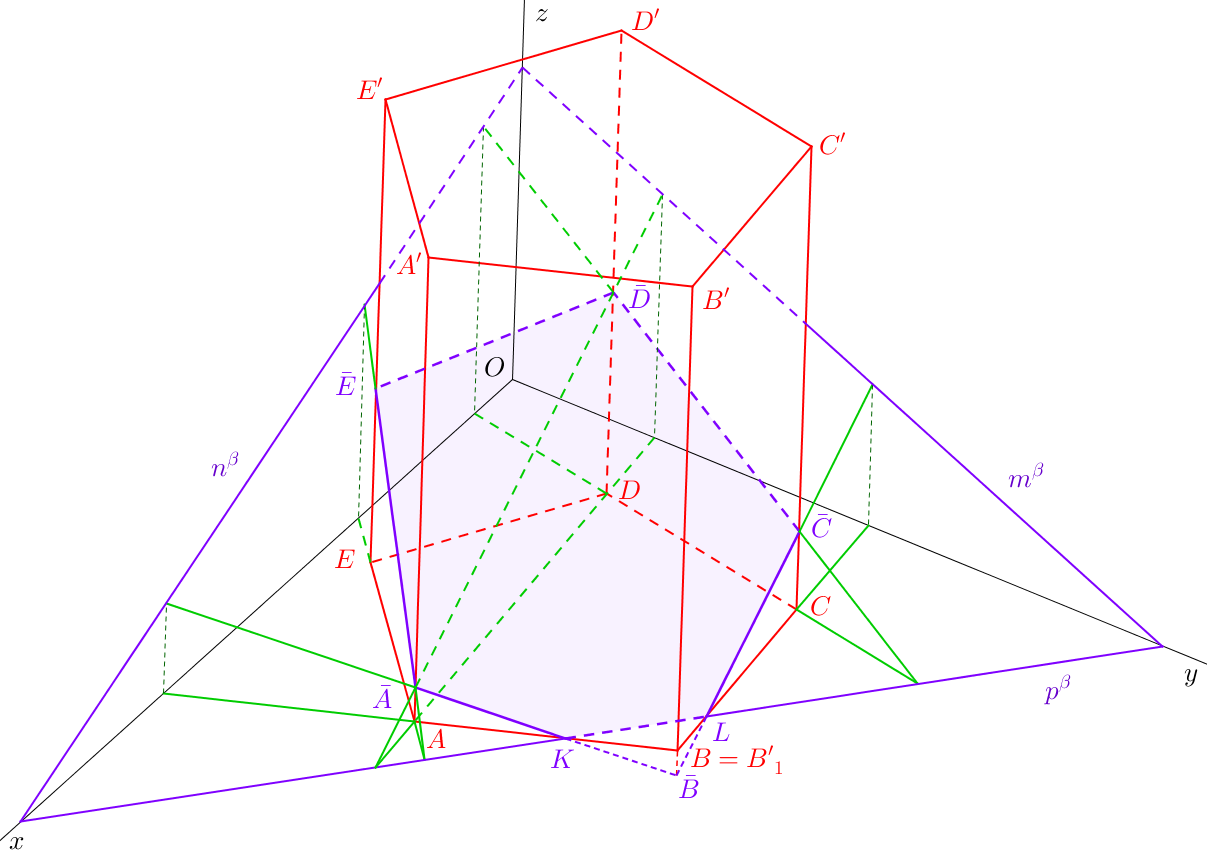

Na obr. 9.1 vidíme kolmý hranol \(ABCDEA'B'C'D'E'\) a rovinu \(\beta\) zadanou svými stopami. Úkolem je sestrojit řez tohoto hranolu rovinou \(\beta\).

Směrem hranolu (a tedy i směrem afinity) je směr bočních hran hranolu, například hrany \(AA'\). Je-li hranol kolmý, afinně sdruženými přímkami k přímkám ležícím v rovině \(\beta\) jsou jejich pravoúhlé průměty do roviny podstavy (na obrázku 9.1 půdorysy - zelené přímky). K určení řezu zvolíme některé z přímek \(AB\), \(BC\), \(CD\), \(DE\), \(AE\), ke kterým pomocí stopníků najdeme přímky afinně sdružené. Průniky roviny \(\beta\) se stěnami řezu tvoří strany řezu. Protíná-li půdorysná stopa roviny řezu podstavu hranolu, tvoří řez rovněž část této stopy ohraničená podstavou (tedy úsečka \(KL\)). Výsledným řezem na obr. 9.1 je šestiúhelník \(\bar{A}KL\bar{C}\bar{D}\bar{E}\).

Stejně jako řešíme viditelnost tělesa, musíme na závěr vyřešit viditelnost řezu. Ohraničuje-li stranu řezu alespoň jedna neviditelná hrana hranolu, je strana řezu neviditelná (na obr. 9.1 se jedná o úsečky \(\bar{C}\bar{D}\) a \(\bar{D}\bar{E}\)). Pro určení viditelnosti ostatních stran řezu si musíme uvědomit, zda strana leží ve stěně hranolu, která je vidět (strany \(\bar{E}\bar{A}\), \(\bar{A}K\), \(L\bar{C}\)), nebo ve stěně, která vidět není (strana \(KL\)).

Stejným způsobem vyřešíme i viditelnost řezů ostatních hranatých těles, proto se jí již dále v textu nezabýváme.

Pamatujme, že rovina řezu může protínat i horní podstavu tělesa. Průsečnici roviny řezu s horní podstavou bychom získali spojením průsečíků lomených čar \(\bar{A}\bar{B}\bar{C}\bar{D}\bar{E}\bar{A}\) a \(A'B'C'D'E'A'\).

Úloha 47. \(X\)[4-10; 7-20], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=6\). Jsou dány body \(A=[6;9;0]\), \(B=[9;3;0]\), \(C=[5;3;0]\), \(D=[5;8;0]\), rovina \(\varrho =(8; \infty ;8)\) a délka \(v=8\). Sestrojte řez kolmého hranolu \(ABCDA'B'C'D'\) rovinou \( \varrho \). Výška hranolu je \(v\).

Úloha 48. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán pravidelný šestiboký hranol \(ABCDEFA'B'C'D'E'F'\) jehož podstava leží v bokorysně. Bod \(A=[0;4;3]\), střed podstavy \(S=[0;4;6]\), výška hranolu \(v = 7\) (viz úloha 37). Sestrojte řez hranolu \(ABCDEFA'B'C'D'E'F'\) rovinou \(\rho = (9;8;14)\). ŘEŠENÍ

Směrem afinity kosého hranolu (obr. 9.2) je rovněž směr bočních hran hranolu. Sdruženými přímkami k přímkám ležícím v rovině řezu však nebudou jejich průměty v rovině podstavy. Než začneme určovat řez hranolu, musíme nejprve najít jeden bod řezu (vyjma samodružných bodů) na libovolné boční hraně.

Na obr. 9.2 je nalezen bod \(\bar{A}\) jako průsečík hrany \(AA'\) s krycí přímkou \(k\) nebo s krycí přímkou \(l\). Nyní již máme zadanou afinitu, s jejíž pomocí řez dokončíme.

Nakonec vyřešíme viditelnost řezu.

Úloha 49. \(X\)[2-6; 3-19], \(\triangle XYZ\): \(|XY|=8\), \(|YZ|=7\), \(|XZ|=8\). Jsou dány body \(A=[8;0;3]\), \(B=[3;0;0]\), \(C=[6;0;6]\), \(A'=[4;6;2]\) a rovina \(\varrho =(8; 9 ;8)\). Sestrojte řez kosého hranolu \(ABCA'B'C'\) rovinou \( \varrho \).