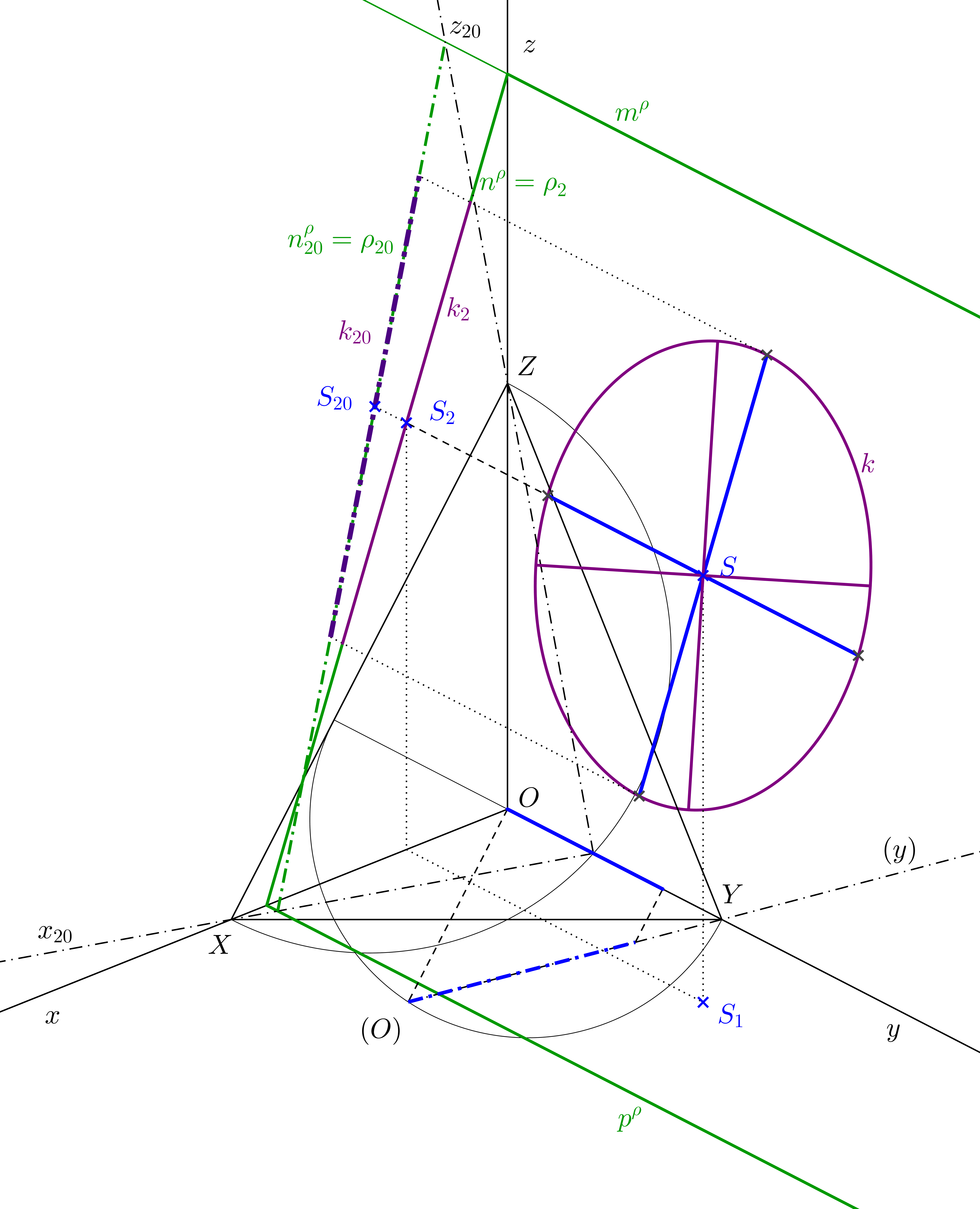
7.6 Kružnice v rovině kolmé k pomocné průmětně

Sestrojme kružnici v rovině, která je kolmá k pomocné průmětně, ale není s žádnou pomocnou průmětnou rovnoběžná. Na obr. 7.6 je rovina \(\rho\) kolmá k nárysně. Nárysem \(\rho_2\) takové roviny je její nárysná stopa \(n^\rho\). Nárysem \(k_2\) kružnice \(k\) je úsečka ležící na stopě \(n^\rho\).

K sestrojení kružnice nejprve otočíme nárysnu a určíme nárys situace. Poté nalezneme sdružené průměry kružnice v axonometrii: délku průměru, který je rovnoběžný s nárysnou (tedy s nárysnou stopou), vidíme v nárysu. Délku průměru kolmého k nárysně určíme např. sklopením promítací roviny osy \(y\), která je s tímto průměrem rovnoběžná. Skutečnou délku poloměru naneseme do sklopení z otočené nárysny. Kružnici \(k\) jsme již schopni sestrojit - můžeme použít příčkovou konstrukci elipsy, případně pomocí Rytzovy konstrukce získat hlavní a vedlejší osu průmětu kružnice \(k\).