Leží-li kružnice v rovině rovnoběžné s axonometrickou průmětnou (resp. v axonometrické průmětně), jejím obrazem je kružnice. Pokud kružnice leží v rovině kolmé k axonometrické průmětně, jejím obrazem je úsečka. V ostatních případech je obrazem kružnice elipsa.

Ukážeme si různé způsoby, jejichž pomocí zobrazíme kružnici ležící v půdorysně do axonometrické půdorysny. Poté si vysvětlíme, jak zobrazit kružnici ležící v nárysně/bokorysně či v rovině rovnoběžné s průmětnou. V závěru této kapitoly zobrazíme kružnici v rovině kolmé k pomocné průmětně.

Postupů, jejichž pomocí lze zobrazit kružnici, není málo. Při konstrukcích můžeme přemýšlet nejen nad tím, jak si zjednodušit práci, ale i nad přesností a přehledností jednotlivých postupů řešení dané úlohy.

7.1 Určení sdružených průměrů z otočené průmětny

Stejně jako u zobrazení mnohoúhelníku (viz kapitola 6) zobrazíme kružnici nejprve v otočené půdorysně (viz kružnice \(k_{0}\) na obr. 7.1), následně ji otočíme zpět do axonometrické půdorysny.

Nejprve si připomeňme, že mezi axonometrickým a otočeným půdorysem existuje afinita, jejíž osou je přímka \(XY\) a směrem axonometrický průmět osy \(z\). O afinním obrazu kružnice víme, že kolmé průměry vzoru (tedy kružnice, kterou chceme zobrazit v afinitě) se zobrazí na sdružené průměry obrazu (tzn. elipsy, která v dané afinitě odpovídá původní kružnici). Zvolíme-li tedy libovolné dva navzájem kolmé průměry \(K_{0}L_{0}\), \(M_{0}N_{0}\) kružnice \(k_{0}\) v otočené půdorysně (obr. 7.2), jejich otočením do axonometrické půdorysny (resp. jejich afinním obrazem) budou sdružené průměry \(KL\), \(MN\) axonometrického průmětu kružnice. Poté pomocí Rytzovy konstrukce najdeme hlavní a vedlejší osu elipsy. Axonometrický průmět bodů kružnice \(k\) dorýsujeme pomocí libovolné konstrukce.

Úloha 29. \(X\)[9; 8-21], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=8\), \(|XZ|=8\). Je dán bod \(S=[8;6;0]\) a délka \(r=10\). V půdorysně sestrojte kružnici se středem \(S\) a poloměrem \(r\).

Úloha 30. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán bod \(S=[8;8;0]\) a délka \(r=3\). V půdorysně sestrojte kružnici se středem \(S\) a poloměrem \(r\).

Úloha 31. \(X\)[3-9; 2-18], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán bod \(S=[0;0;0]\) a délka \(r=3\). V půdorysně sestrojte kružnici se středem \(S\) a poloměrem \(r\).

7.2 Využití afinity

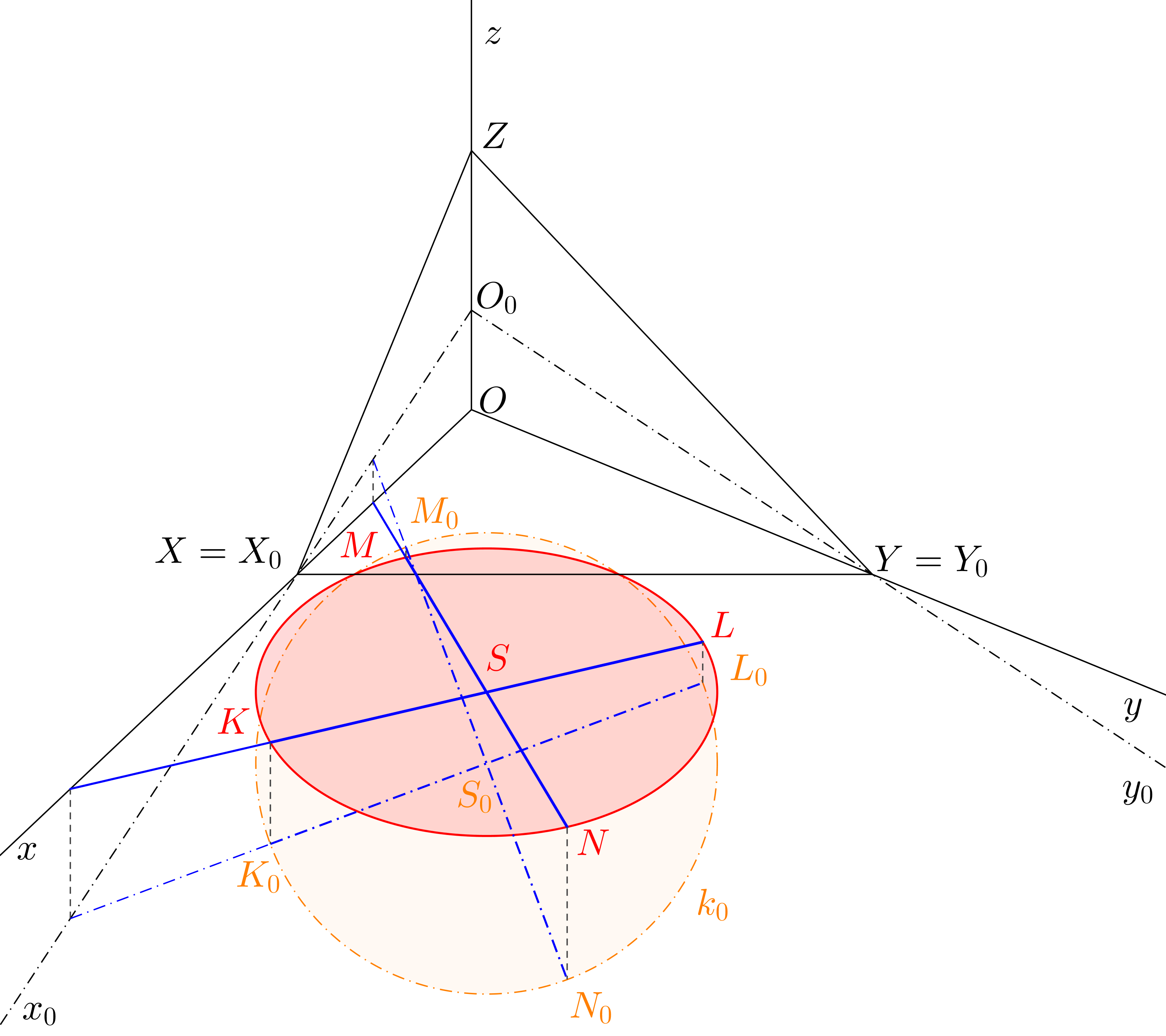
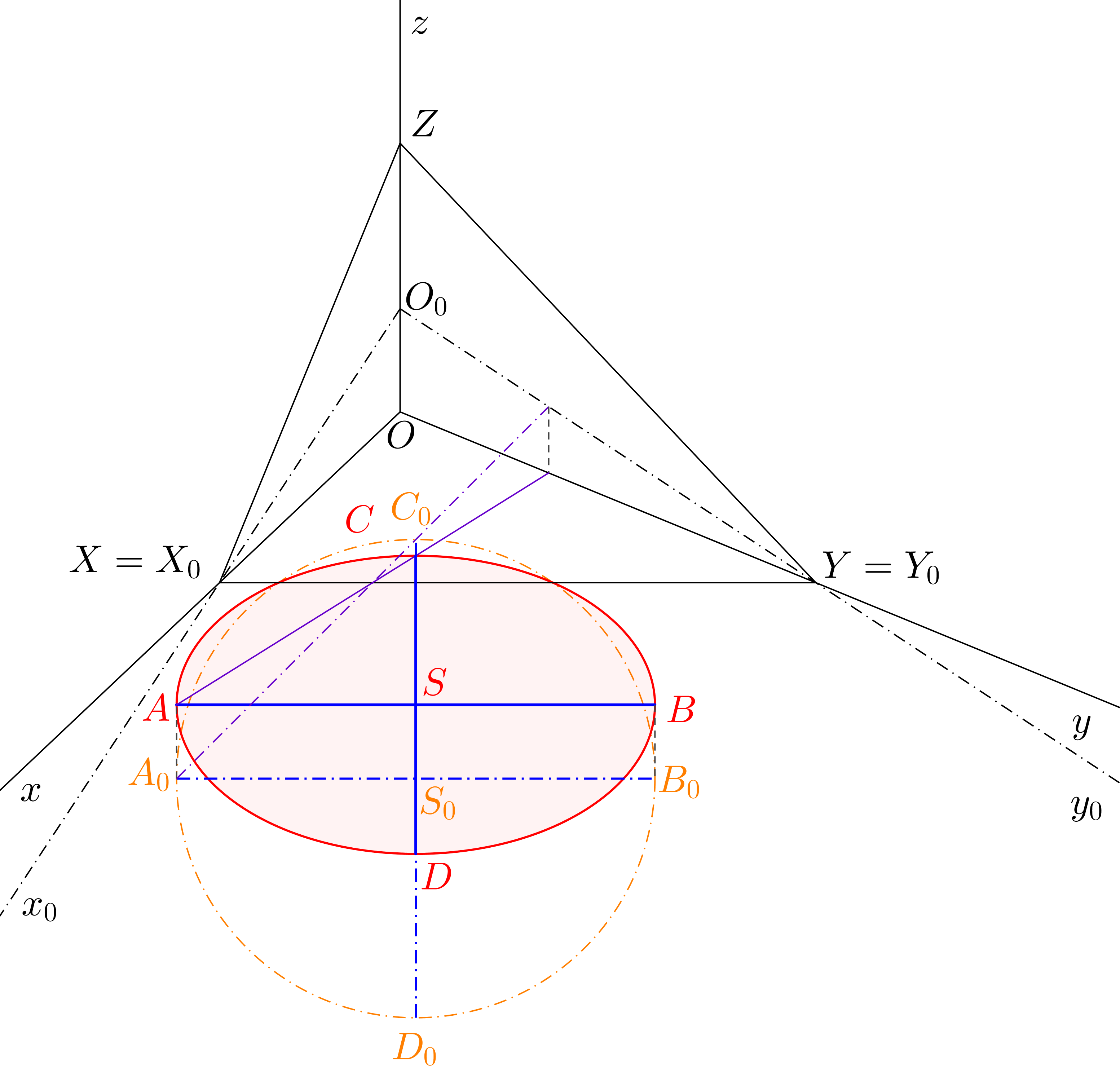
Afinita mezi otočenou půdorysnou a axonometrickou půdorysnou nám však může usnadnit práci ještě více. Víme, že přímky rovnoběžné s osou afinity se zobrazí opět na rovnoběžky s touto osou. Pokud tedy kolmé průměry \(A_{0}B_{0}\), \(C_{0}D_{0}\) zvolíme tak, aby průměr \(A_{0}B_{0}\) byl rovnoběžný s osou afinity (viz obr. 7.3, v našem případě je osou afinity přímka \(XY\)), obrazem těchto průměrů budou přímo hlavní osa \(AB\) a vedlejší osa \(CD\) axonometrického průmětu kružnice (tedy osy elipsy, kterou chceme zobrazit).

Podívejme se nyní pozorně na obr. 7.3. Axonometrické průměty bodů \(A\), \(C\) můžeme získat snadno zobrazením axonometrického průmětu přímky \(AC\) (otočením fialové přímky \(A_{0}C_{0}\) do axonometrické půdorysny získáme přímku \(AC\), body \(A\), \(C\) poté ve směru afinity z bodů \(A_0\), \(C_0\)). Víme, že hlavní osa \(AB\) je rovnoběžná s přímkou \(XY\), vedlejší osa \(CD\) musí být kolmá na hlavní osu \(AB\) (v našem případě musí ležet na přímce \(C_{0}D_{0}\)). V průsečíku os \(AB\), \(CD\) najdeme střed \(S\). Vrcholy \(B\), \(D\) jsou středově souměrné s body \(A\), \(C\) podle středu \(S\).

Úloha 32. Zobrazte kružnice dle zadání v úlohách 29, 30, 31. Použijte afinitu.

7.3 Užití Thalétovy věty

Nyní si ukážeme konstrukci, k níž nepotřebujeme konstruovat kružnici v otočené půdorysně. Stačí nám najít její střed \(S\) (resp. bod \(A\) nebo \(B\)) a zobrazit průměr \(AB\).

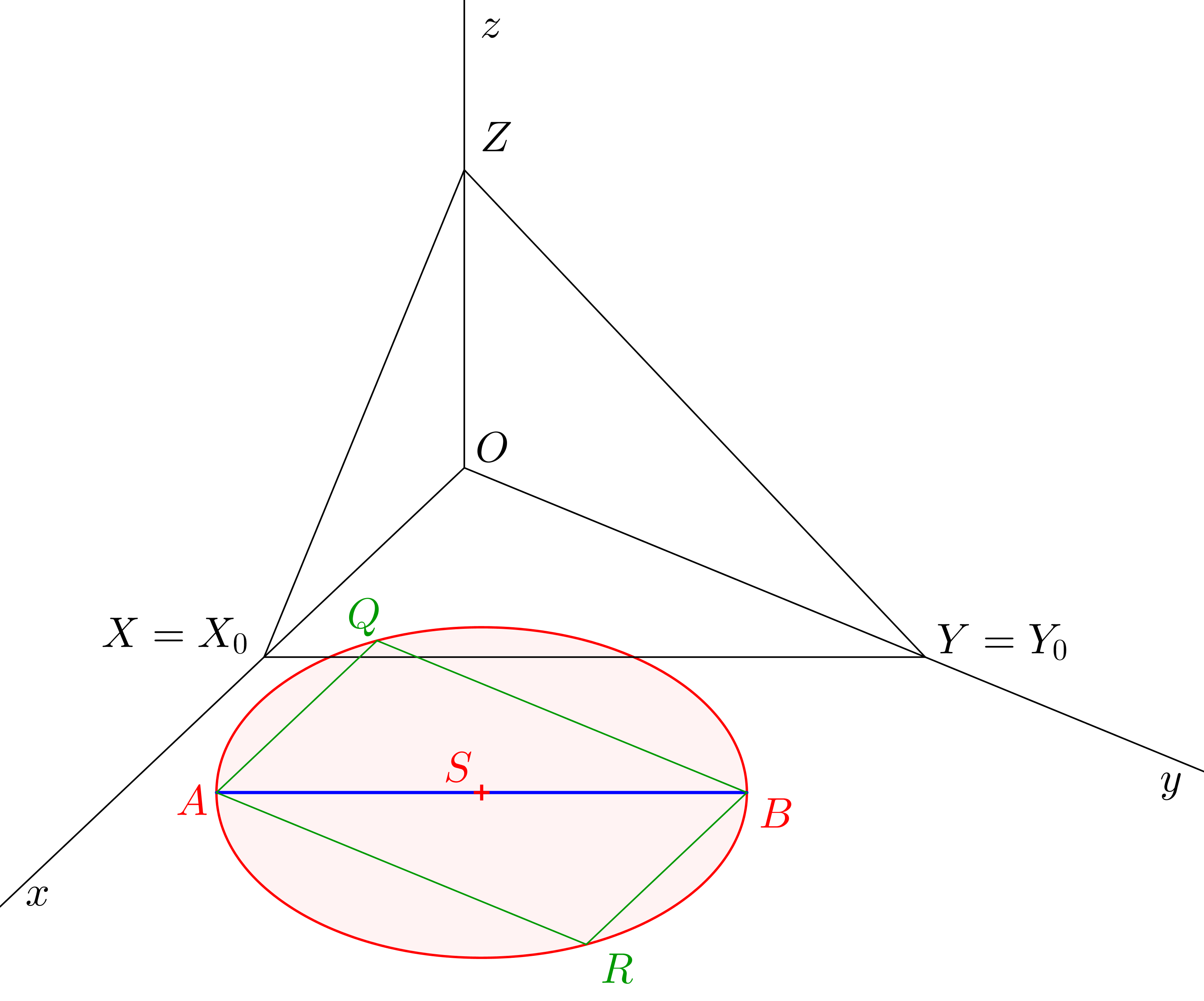
Na obr 7.3 si můžeme všimnout, že kružnice \(k_{0}\) je tzv. Thalétova kružnice nad průměrem \(A_{0}B_{0}\). V půdorysně známe dvě ve skutečnosti navzájem kolmé přímky: osy \(x\), \(y\). V průsečících rovnoběžek s osami \(x\), \(y\) z bodů \(A\), \(B\) tedy najdeme body \(Q\), \(R\) elipsy (obr 7.4, stačí nám jeden z nich). Vedlejší vrcholy elipsy poté získáme pomocí proužkové konstrukce.

Úloha 33. Zobrazte kružnice dle zadání v úlohách 29, 30, 31. Použijte Thalétovu kružnici. ŘEŠENÍ ÚLOH 33/30, 33/31

7.4 Vysunutí sklopené pomocné průmětny

Podívejme se na metodu, jejíž pomocí si můžeme zjednodušit konstrukci rotačních těles. Ukážeme si, jak zobrazit kružnici v půdorysně se středem v počátku soustavy souřadnic vysunutím sklopené pomocné průmětny - promítací roviny osy \(z\) (obr. 7.5).

Sklopíme-li promítací rovinu osy \(z\), půdorysna \(\pi\) se v tomto sklopení jeví jako přímka. Sklopenou osu \(z\) i sklopenou půdorysnu, tj, přímky \((z)\) a \((\pi)\), nyní posuneme libovolně daleko ve směru kolmém k ose \(z\) - viz přímky \((z)'\), \((\pi)'\). V takto vysunuté rovině \((\pi)'\) zobrazíme kružnici. Jelikož kružnice leží v rovině \(\pi\), zobrazí se na úsečku. Středem úsečky bude střed kružnice, tedy vysunutý počátek \((O)'\), délkou úsečky průměr kružnice. Krajní body úsečky označme \((C)'\), \((D)'\). Z bodů \((C)'\), \((D)'\) spustíme kolmice k průmětu osy \(z\). Průsečíky těchto kolmic s osou \(z\) budou krajní body \(C\), \(D\) vedlejší osy elipsy, na níž se kružnice v axonometrii zobrazí. Krajní body \(A\), \(B\) hlavní osy elipsy budou ležet na přímce kolmé k průmětu osy \(z\) procházející počátkem \(O\). Protože úsečka \(AB\) leží v rovině rovnoběžné s axonometrickou průmětnou, zobrazí se průměr \(AB\) ve skutečné velikosti, tzn. délky úseček \(AO\), \(OB\) jsou rovny poloměru kružnice.

Úloha 34. Zobrazte kružnice dle zadání v úlohách 29, 30, 31. Úlohy řešte vysunutím sklopené promítací roviny osy \(z\).

7.5 Kružnice v dalších rovinách

Pro zobrazení kružnice ležící v nárysně/bokorysně použijeme stejný postup jako pro zobrazení kružnice ležící v půdorysně. Do axonometrické průmětny otočíme rovinu, ve které kružnice leží. Při užití Thalétovy věty sestrojíme rovnoběžky s osami ležícími v této rovině. Chceme-li sklopit a vysunout pomocnou průmětnu, zvolíme průmětnu, která je kolmá k rovině, v níž kružnice leží.

Úloha 35. \(X\)[5-9; 2-16], \(\triangle XYZ\): \(|XY|=5\), \(|YZ|=6\), \(|XZ|=7\). Je dán bod \(S=[2;0;7]\) a délka \(r=6\). V bokorysně sestrojte kružnici se středem \(S\) a poloměrem \(r\).

Pro zobrazení kružnice v rovině rovnoběžné s půdorysnou/nárysnou/bokorysnou zobrazíme nejprve kružnici v půdorysně/nárysně/bokorysně. Takto zobrazenou kružnici následně posuneme do správné roviny (stejně, jako je tomu u mnohoúhelníků, viz obr. 6.4). Pokud jsme sklopili promítací rovinu, máme již sklopenou i osu \(z\)/\(y\)/\(x\) a nemusíme ji znovu sklápět.

Úloha 36. \(X\)[7-10; 11-17], \(\triangle XYZ\): \(|XY|=7\), \(|YZ|=7\), \(|XZ|=9\). Je dán bod \(S=[9;9;8]\) a délka \(r=7\). V rovině rovnoběžné s půdorysnou sestrojte kružnici se středem \(S\) a poloměrem \(r\).

7.6 Kružnice v rovině kolmé k pomocné průmětně

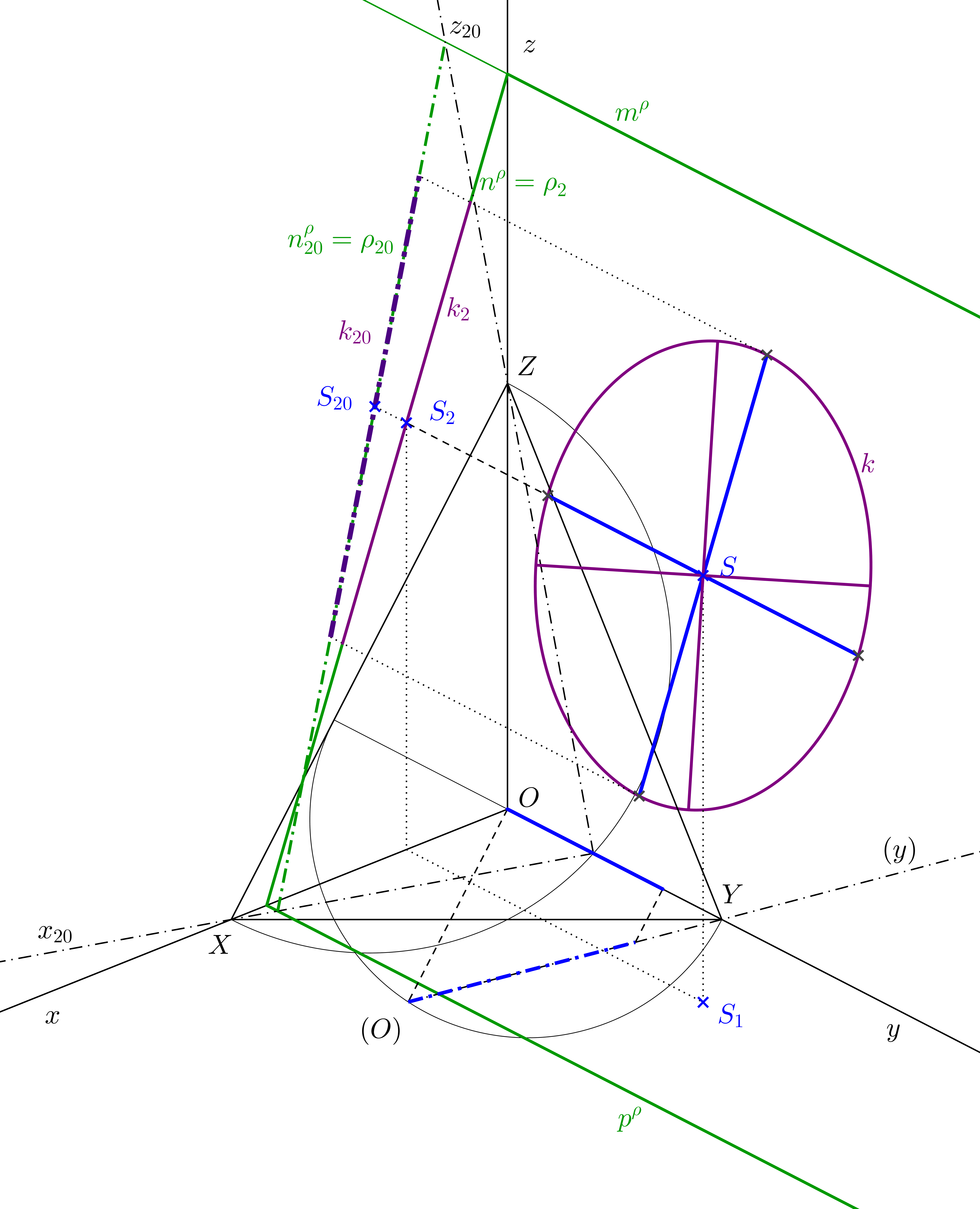
Sestrojme kružnici v rovině, která je kolmá k pomocné průmětně, ale není s žádnou pomocnou průmětnou rovnoběžná. Na obr. 7.6 je rovina \(\rho\) kolmá k nárysně. Nárysem \(\rho_2\) takové roviny je její nárysná stopa \(n^\rho\). Nárysem \(k_2\) kružnice \(k\) je úsečka ležící na stopě \(n^\rho\).

K sestrojení kružnice nejprve otočíme nárysnu a určíme nárys situace. Poté nalezneme sdružené průměry kružnice v axonometrii: délku průměru, který je rovnoběžný s nárysnou (tedy s nárysnou stopou), vidíme v nárysu. Délku průměru kolmého k nárysně určíme např. sklopením promítací roviny osy \(y\), která je s tímto průměrem rovnoběžná. Skutečnou délku poloměru naneseme do sklopení z otočené nárysny. Kružnici \(k\) jsme již schopni sestrojit - můžeme použít příčkovou konstrukci elipsy, případně pomocí Rytzovy konstrukce získat hlavní a vedlejší osu průmětu kružnice \(k\).