7.3 Užití Thalétovy věty

Nyní si ukážeme konstrukci, k níž nepotřebujeme konstruovat kružnici v otočené půdorysně. Stačí nám najít její střed \(S\) (resp. bod \(A\) nebo \(B\)) a zobrazit průměr \(AB\).

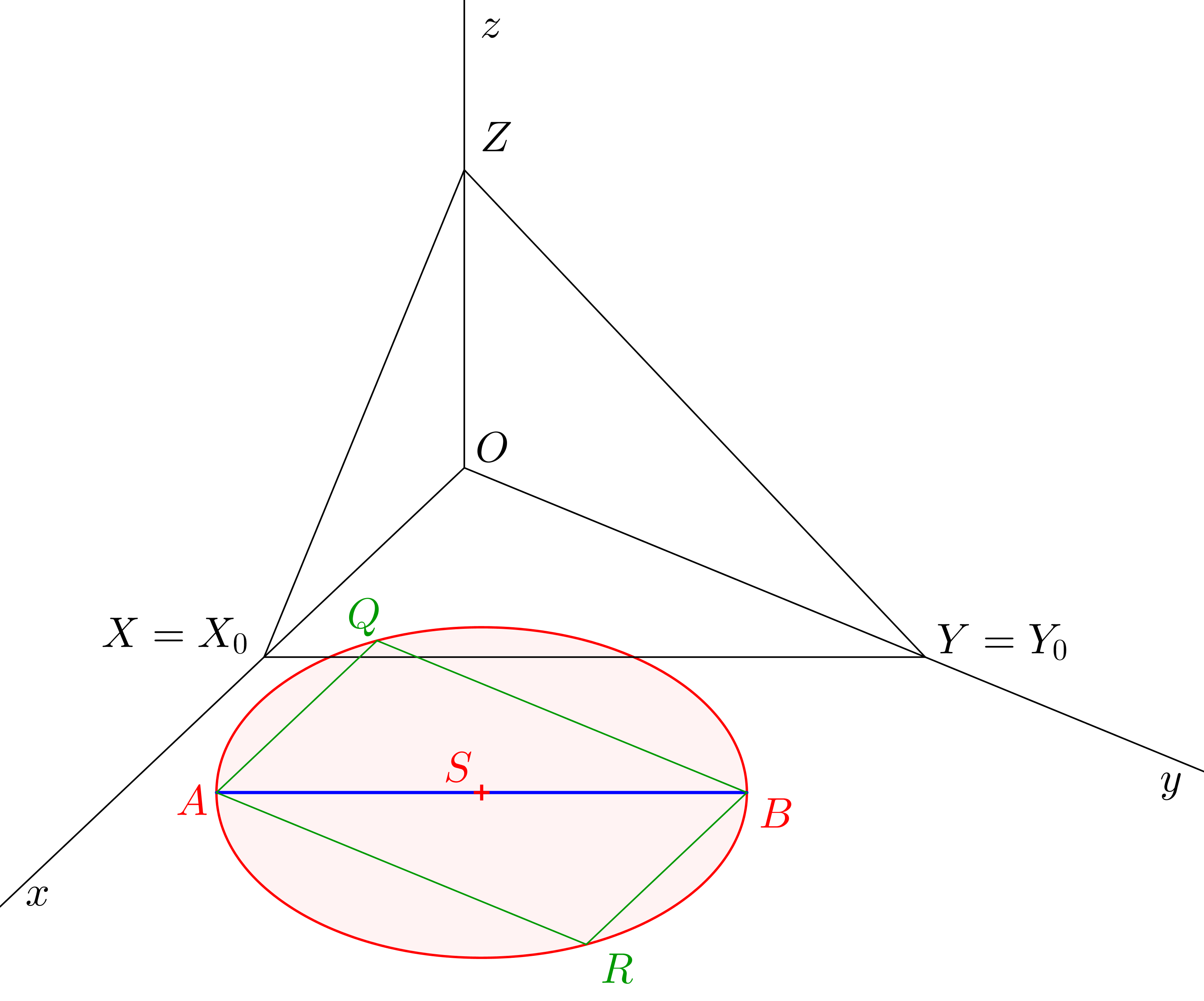
Na obr 7.3 si můžeme všimnout, že kružnice \(k_{0}\) je tzv. Thalétova kružnice nad průměrem \(A_{0}B_{0}\). V půdorysně známe dvě ve skutečnosti navzájem kolmé přímky: osy \(x\), \(y\). V průsečících rovnoběžek s osami \(x\), \(y\) z bodů \(A\), \(B\) tedy najdeme body \(Q\), \(R\) elipsy (obr 7.4, stačí nám jeden z nich). Vedlejší vrcholy elipsy poté získáme pomocí proužkové konstrukce.

Úloha 33. Zobrazte kružnice dle zadání v úlohách 29, 30, 31. Použijte Thalétovu kružnici. ŘEŠENÍ ÚLOH 33/30, 33/31