7.2 Využití afinity

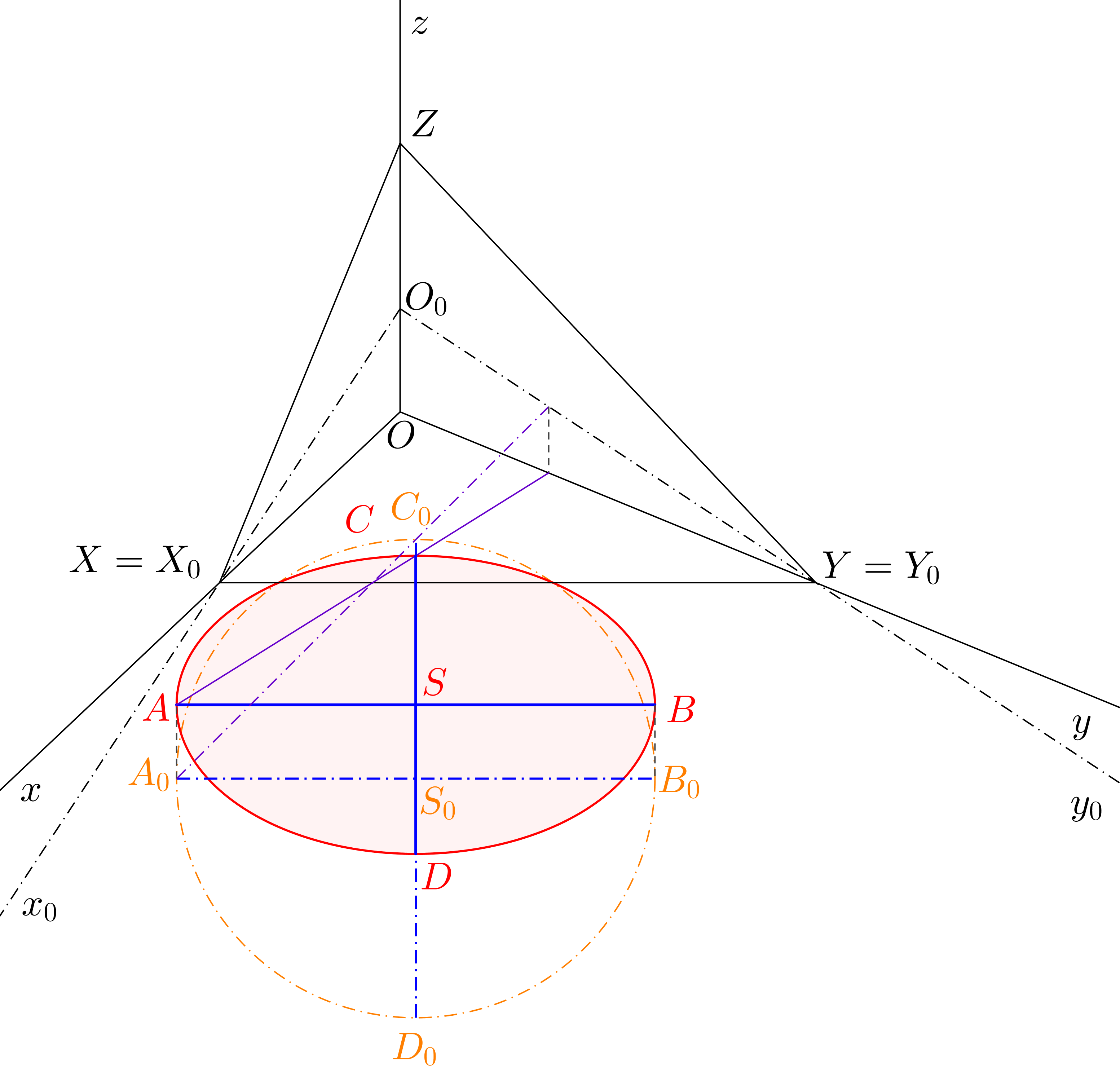
Afinita mezi otočenou půdorysnou a axonometrickou půdorysnou nám však může usnadnit práci ještě více. Víme, že přímky rovnoběžné s osou afinity se zobrazí opět na rovnoběžky s touto osou. Pokud tedy kolmé průměry \(A_{0}B_{0}\), \(C_{0}D_{0}\) zvolíme tak, aby průměr \(A_{0}B_{0}\) byl rovnoběžný s osou afinity (viz obr. 7.3, v našem případě je osou afinity přímka \(XY\)), obrazem těchto průměrů budou přímo hlavní osa \(AB\) a vedlejší osa \(CD\) axonometrického průmětu kružnice (tedy osy elipsy, kterou chceme zobrazit).

Podívejme se nyní pozorně na obr. 7.3. Axonometrické průměty bodů \(A\), \(C\) můžeme získat snadno zobrazením axonometrického průmětu přímky \(AC\) (otočením fialové přímky \(A_{0}C_{0}\) do axonometrické půdorysny získáme přímku \(AC\), body \(A\), \(C\) poté ve směru afinity z bodů \(A_0\), \(C_0\)). Víme, že hlavní osa \(AB\) je rovnoběžná s přímkou \(XY\), vedlejší osa \(CD\) musí být kolmá na hlavní osu \(AB\) (v našem případě musí ležet na přímce \(C_{0}D_{0}\)). V průsečíku os \(AB\), \(CD\) najdeme střed \(S\). Vrcholy \(B\), \(D\) jsou středově souměrné s body \(A\), \(C\) podle středu \(S\).

Úloha 32. Zobrazte kružnice dle zadání v úlohách 29, 30, 31. Použijte afinitu.