Chceme-li sestrojit průmět přímky, zobrazíme dva její body, kterými proložíme přímku. Pro přímku \(p=KL\) zobrazíme body \(K\), \(K_{1}\), \(L\), \(L_{1}\). Přímka \(KL\) je axonometrickým průmětem přímky \(p\), přímka \(K_{1}L_{1}\) axonometrickým půdorysem \(p_{1}\) přímky \(p\) (obr. 4.1).

Je-li přímka kolmá k axonometrické rovině, jejím axonometrickým půdorysem bude přímka rovnoběžná s axonometrickou osou \(z\). Axonometrickým průmětem bude bod ležící na axonometrickém půdorysu.

Úloha 12. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Jsou dány body \(N^{m}=[5;0;5]\), \(M^{m}=[0;9;7]\). Zobrazte přímku \(m= \leftrightarrow N^{m}M^{m}\).

Stopník přímky je průsečík přímky s průmětnou. Přímky mohou mít čtyři stopníky. Jsou jimi axonometrický stopník \(A\), půdorysný stopník \(P\), nárysný stopník \(N\) a bokorysný stopník \(M\). Tyto stopníky jsou průsečíky přímky s axonometrickou rovinou \(\alpha\), půdorysnou \(\pi\), nárysnou \(\nu\) a bokorysnou \(\mu\).

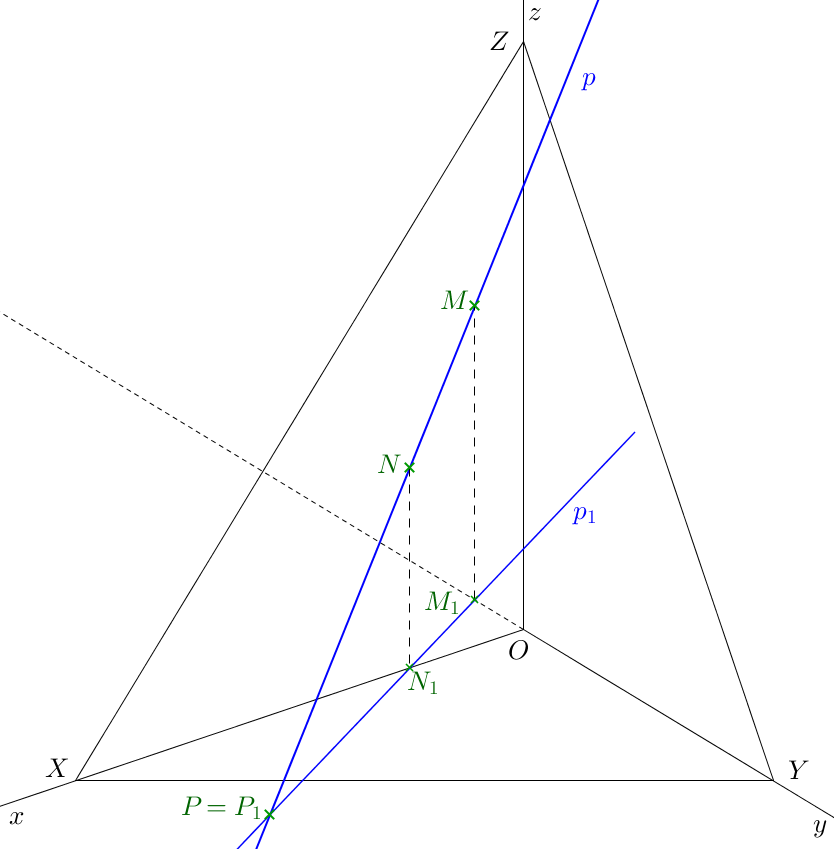
Půdorysný stopník \(P\) přímky \(p\) je v pravoúhlé axonometrii vidět ihned, bez další konstrukce (obr. 4.2). Jedná se o průsečík axonometrického průmětu a axonometrického půdorysu dané přímky. Axonometrický půdorys \(P_{1}\) půdorysného stopníku splývá s jeho axonometrickým průmětem \(P\).

Axonometrickým půdorysem nárysného stopníku \(N\) je průsečík \(N_{1}\) axonometrického půdorysu \(p_{1}\) přímky \(p\) a osy \(x\). Jeho axonometrický průmět najdeme na ordinále na axonometrickém průmětu přímky \(p\). Podobně postupujeme i při hledání bokorysného stopníku \(M\) - nejprve najdeme axonometrický půdorys \(M_{1}\) jako průsečík axonometrického půdorysu \(p_{1}\) přímky \(p\) s osou \(y\). Axonometrický průmět \(M\) bokorysného stopníku leží na ordinále z bodu \(M_1\) a na axonometrickém průmětu přímky \(p\).

Axonometrický stopník přímky si ukážeme v kapitole 5.2.

Úloha 13. \(X\)[5-13; 3-20], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Jsou dány body \(N^{q}=[7;0;6]\), \(M^{q}=[0;6;6]\). Zobrazte přímku \(q= \leftrightarrow N^{q}M^{q}\). Určete její půdorysný stopník.

Úloha 14. \(X\)[2-7; 7-18], \(\triangle XYZ\): \(|XY|=13\), \(|YZ|=6\), \(|XZ|=12\). Jsou dány body \(D=[12;3;14]\), \(E=[3;1;2]\). Sestrojte stopníky přímky \(p= \leftrightarrow DE\).

Úloha 15. \(X\)[5-15; 5-20], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Jsou dány body \(A=[2;3;6]\), \(B=[5;0,8;3]\) Určete stopníky přímky \(a= \leftrightarrow AB\).

4.1 Bod na přímce

Bod \(K\) leží na přímce \(p\) právě tehdy, když jeho axonometrický průmět  \(K\) leží na axonometrickém průmětu \(p\) přímky a axonometrický půdorys \(K_{1}\) bodu \(K\) leží na axonometrickém půdorysu \(p_{1}\) přímky \(p\) (obr. 4.3). V opačném případě bod \(K\) neleží na přímce \(p\).

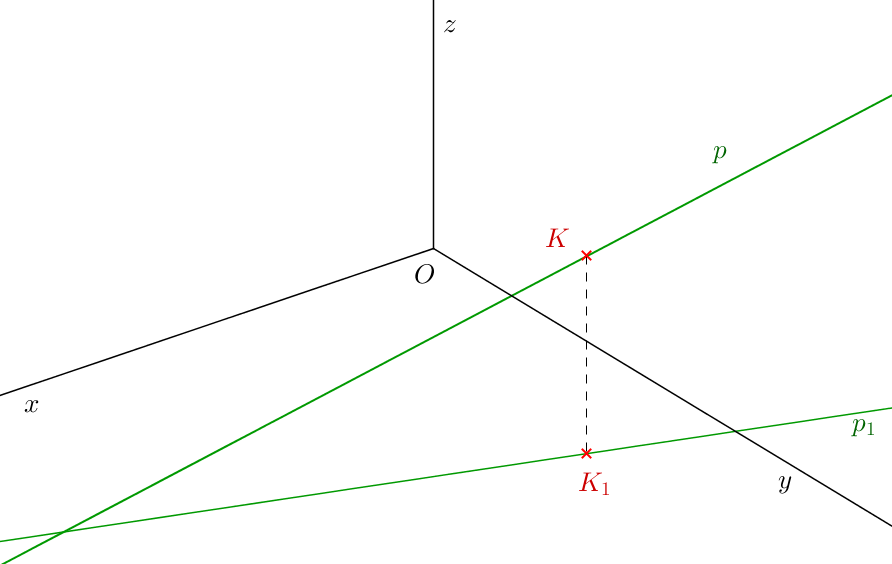
4.2 Dvě přímky

Dvě přímky \(p\), \(q\) (obr. 4.4) jsou navzájem rovnoběžné, jsou-li rovnoběžné jejich axonometrické půdorysy i axonometrické průměty.

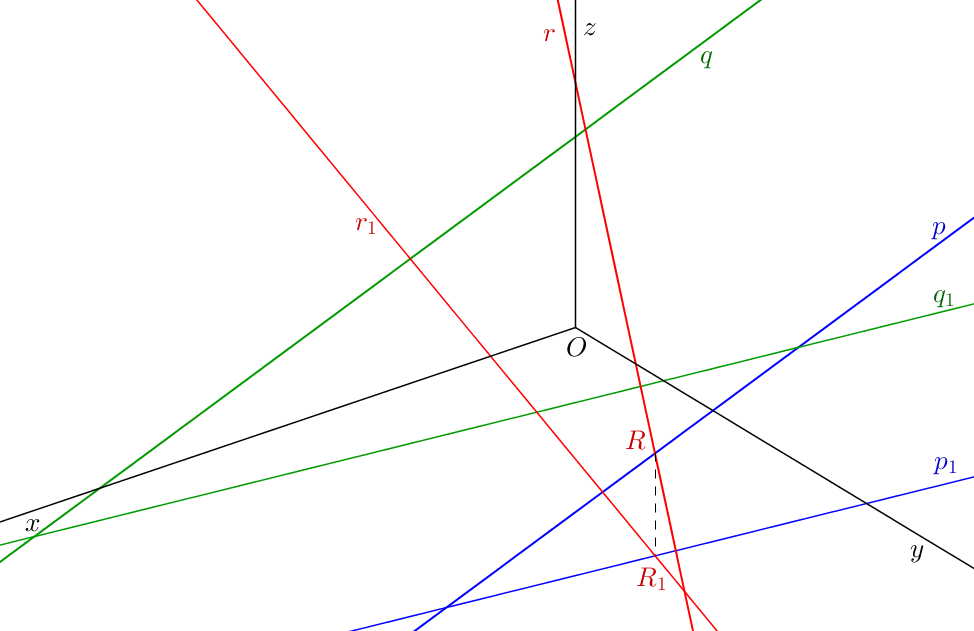
Nejsou-li přímky navzájem rovnoběžné, mohou být různoběžné nebo mimoběžné. Abychom zjistili, zda jsou dvě přímky \(p\), \(r\) (obr. 4.4) různoběžné, musíme najít průsečík jejich axonometrických průmětů \(R\) a průsečík jejich axonometrických půdorysů \(R_{1}\). Leží-li body \(R\), \(R_{1}\) na ordinále, přímky jsou různoběžné a nalezené body jsou axonometrickým průmětem a axonometrickým půdorysem průsečíku těchto přímek. Pokud body \(R\), \(R_{1}\) na ordinále neleží, znamená to, že přímky nemají žádný společný bod, tedy jsou mimoběžné (na obr. 4.4 jsou mimoběžné přímky \(q\), \(r\)).

Úloha 16. \(X\)[6-13; 10-18], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=8\), \(|XZ|=8\). Jsou dány body \(A=[5;7;9]\), \(B=[1;7;2]\), \(C=[12;3;5]\), \(D=[8;3;-2]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).

Úloha 17. \(X\)[1; 8-15], \(\triangle XYZ\): \(|XY|=15\), \(|YZ|=10\), \(|XZ|=14\). Jsou dány body \(A=[8;11;4]\) \(B=[8;14;7]\), \(C=[4;3;12]\), \(D=[5;5;10]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).

Úloha 18. \(X\)[4-8; 5-14], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=6\). Jsou dány body \(A=[3;2;2]\), \(B=[4;-2;14]\), \(C=[1;12;3]\), \(D=[2;8;15]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).