Strana 3 z 3
4.2 Dvě přímky
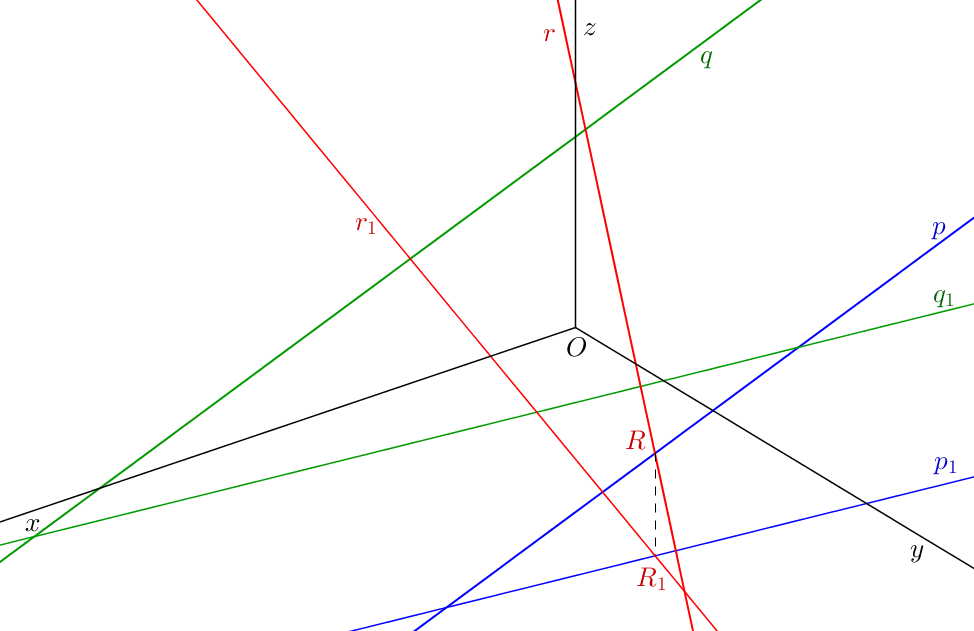
Nejsou-li přímky navzájem rovnoběžné, mohou být různoběžné nebo mimoběžné. Abychom zjistili, zda jsou dvě přímky \(p\), \(r\) (obr. 4.4) různoběžné, musíme najít průsečík jejich axonometrických průmětů \(R\) a průsečík jejich axonometrických půdorysů \(R_{1}\). Leží-li body \(R\), \(R_{1}\) na ordinále, přímky jsou různoběžné a nalezené body jsou axonometrickým průmětem a axonometrickým půdorysem průsečíku těchto přímek. Pokud body \(R\), \(R_{1}\) na ordinále neleží, znamená to, že přímky nemají žádný společný bod, tedy jsou mimoběžné (na obr. 4.4 jsou mimoběžné přímky \(q\), \(r\)).
Úloha 16. \(X\)[6-13; 10-18], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=8\), \(|XZ|=8\). Jsou dány body \(A=[5;7;9]\), \(B=[1;7;2]\), \(C=[12;3;5]\), \(D=[8;3;-2]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).
Úloha 17. \(X\)[1; 8-15], \(\triangle XYZ\): \(|XY|=15\), \(|YZ|=10\), \(|XZ|=14\). Jsou dány body \(A=[8;11;4]\) \(B=[8;14;7]\), \(C=[4;3;12]\), \(D=[5;5;10]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).
Úloha 18. \(X\)[4-8; 5-14], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=6\). Jsou dány body \(A=[3;2;2]\), \(B=[4;-2;14]\), \(C=[1;12;3]\), \(D=[2;8;15]\). Určete vzájemnou polohu přímek \(p = AB\) a \(q = CD\).
