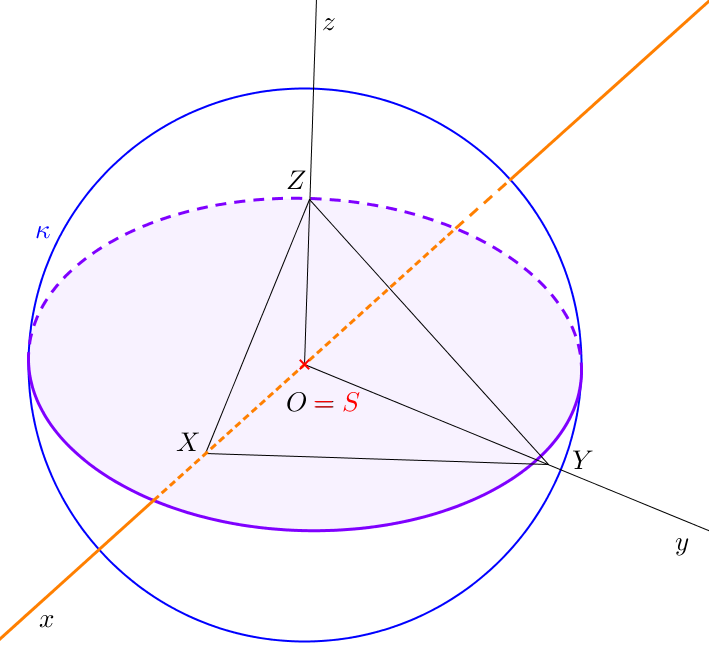
10.2 Průnik přímky s rotačním tělesem

Průnik přímky s rotačním tělesem najdeme stejně jako průnik přímky s mnohostěnem: zvolíme rovinu, která danou přímku obsahuje, a sestrojíme řez tělesa touto rovinou. Průnikem přímky s tělesem je její průnik s řezem. Vzhledem k obtížnější konstrukci řezu je ale nevýhodné volit u válců/kuželů jinou rovinu, než směrovou/vrcholovou (obr. 10.3 a 10.4).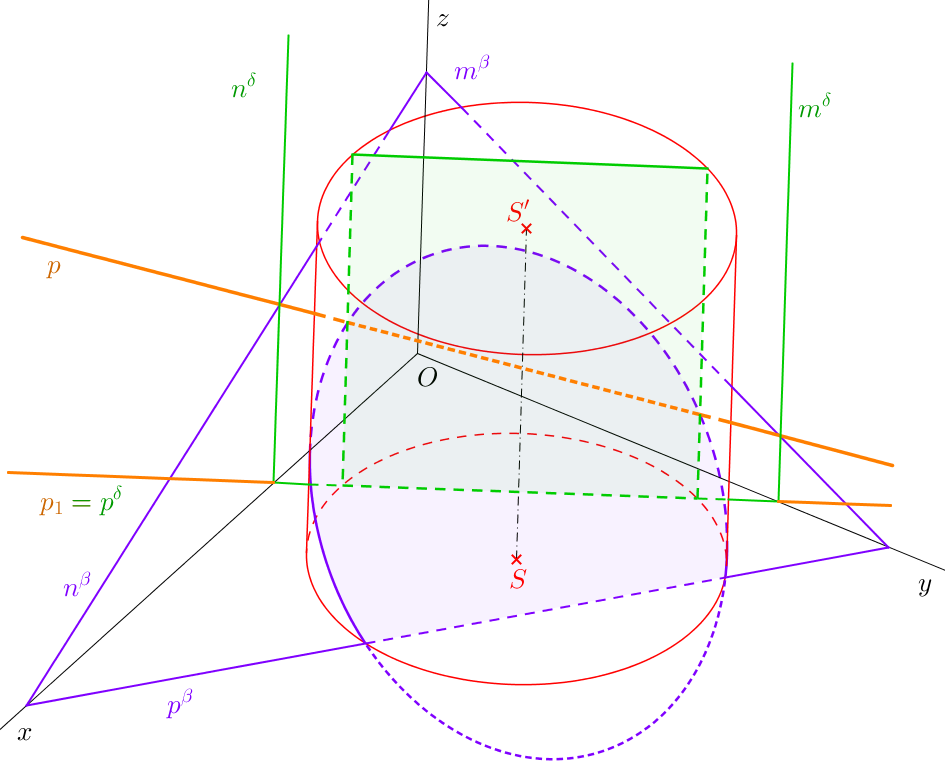

Na obr. 10.3 je zobrazen průnik přímky \(p\) s rotačním válcem. Můžeme si všimnout dvou různých řezů. Řez obecnou rovinou \(\beta\) vede k řešení průniku, konstrukce řezu je ale velmi náročná (je třeba sestrojit elipsu a následně průsečíky elipsy s přímkou). Při volbě směrové roviny \(\delta\) je řezem rotačního válce obdélník (zobrazí se jako kosodélník). Vyhneme se tak konstrukci kuželosečky.

Úloha 58. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán rotační válec, jehož podstava se středem \(S = [8;8;0]\) a poloměrem \(r=3\) leží v půdorysně, výška válce je \(v=7\) (viz úloha 43). Dále jsou dány bod \(N=[6;0;7]\), \(L=[8;9;3]\). Sestrojte průnik válce s přímkou \(k = \leftrightarrow NL\). ŘEŠENÍ

Úloha 59. \(X\)[4-9; 6-19], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=9\). Jsou dány body \(S=[2;0;1]\), \(K=[4;2;1]\), \(L=[1;1;8]\) a délky \(r=6\), \(v=5\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v nárysně. Výška válce je \(v\). Sestrojte průnik válce s přímkou \(KL\).

Řešení průniku přímky \(p\) s kuželem vidíme na obr. 10.4. Jednou možností je použít libovolnou rovinu \(\beta\), jejímž řezem je kuželosečka, kterou následně musíme sestrojit, abychom našli průnik přímky s kuželem. Nebo můžeme přímkou \(p\) proložit vrcholovou rovinu \(\delta\). Řezem kužele rovinou \(\delta\) je trojúhelník.

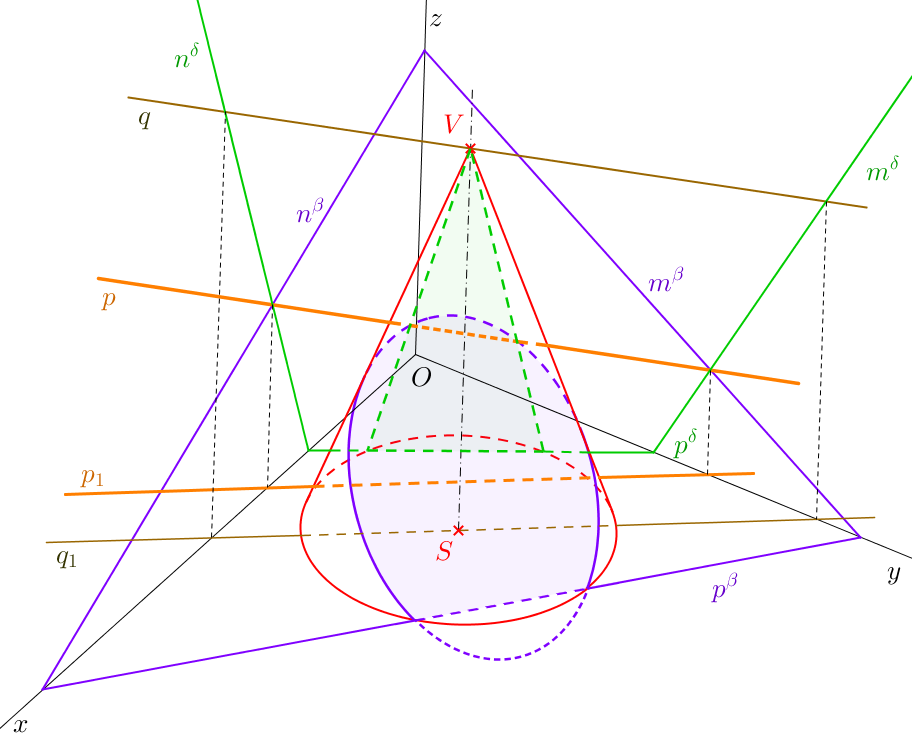
Úloha 60. \(X\)[3-9; 2-18], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán rotační kužel s podstavou v půdorysně. Střed podstavy \(S=[0;0;0]\), poloměr podstavy \(r=3\), výška kužele \(v=10\) (viz úloha 45). Dále jsou dány body \(M=[0;4;6]\), \(N=[1;0;4]\). Sestrojte průnik kužele s přímkou \(l=\leftrightarrow MN\). ŘEŠENÍ

Ukažme si ještě průnik osy \(x\) s koulí, jejíž střed je v počátku \(O\) (obr. 10.5). Mohli bychom sestrojit řez koule půdorysnou či nárysnou a najít průnik s osou \(x\) pomocí tohoto řezu. Tím bychom si ale zbytečně zkomplikovali práci. Uvědomme si, že průsečíky přímky s povrchem koule leží na ose a jejich vzdálenost od středu koule je poloměrem koule. Stačí tedy do axonometrické průmětny sklopit promítací rovinu osy \(x\) nebo otočit půdorysnu/nárysnu. Ze sklopení (otočení) přeneseme skutečnou délku poloměru na axonometrickou osu \(x\).