Průnikem přímky s tělesem rozumíme množinu bodů, které jsou společné přímce i tělesu. Pokud přímka nemá s tělesem společné body, nedochází k průniku. Průnikem může být jeden bod (přímka se dotýká tělesa v jednom bodě na povrchu tělesa) nebo úsečka. Ta může být částí povrchu tělesa. V této kapitole se budeme věnovat průnikům, při kterých je průnikem úsečka procházející vnitřkem tělesa. Jejími krajními body jsou průsečíky přímky se stěnami tělesa.

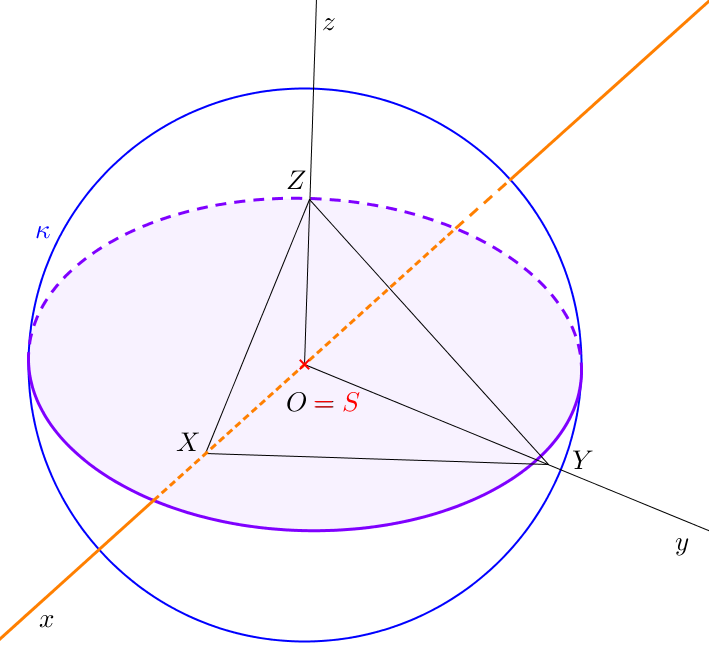
Průnik přímky s tělesem určíme tak, že danou přímkou proložíme libovolnou rovinu a sestrojíme řez tělesa touto rovinou. Body, ve kterých přímka protíná hranici řezu, určují průnik přímky s tělesem.

Budeme se zabývat i vhodností rovin zvolených k pomocnému řezu. Pro průniky jehlanů a kuželů ukážeme volbu vrcholové roviny, průniky hranolů a válců vyřešíme pomocí směrových rovin.

10.1 Průnik přímky s mnohostěnem

Na obr. 10.1 vidíme jehlan \(ABCDEV\) a přímku \(p\). Přímkou \(p\) jsou proloženy roviny \(\beta\) a \(\delta\). Dále jsou sestrojeny řezy jehlanu těmito rovinami. Můžeme si všimnout, že oba řezy protíná přímka \(p\) ve stejné úsečce. Tato úsečka je průnikem přímky s jehlanem.

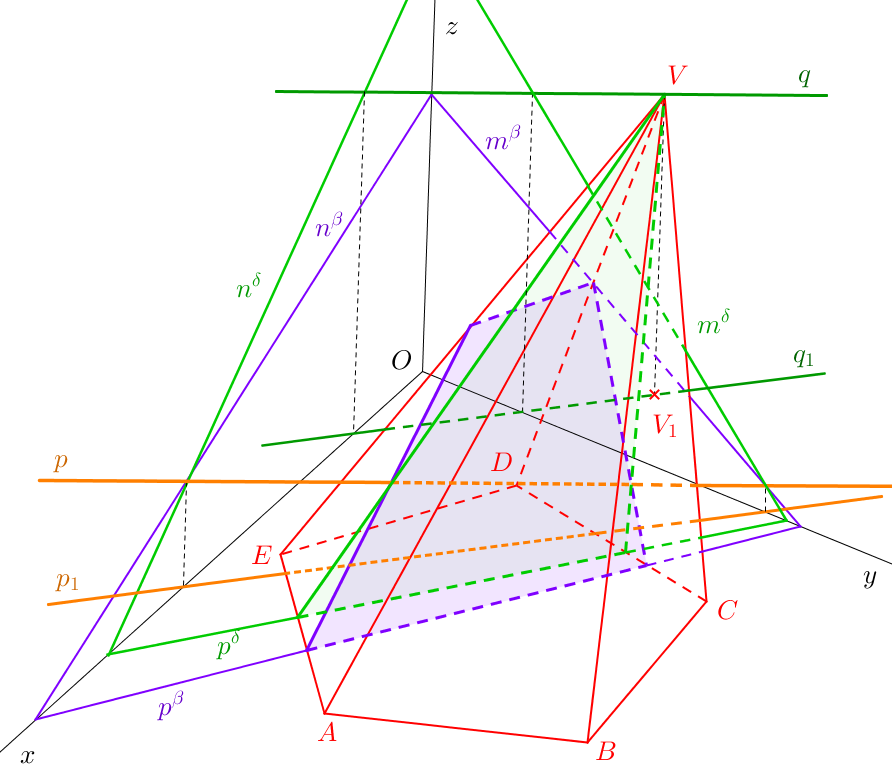
K nalezení průniku přímky \(p\) s jehlanem proložíme přímkou \(p\) libovolnou rovinu \(\beta\) a sestrojíme řez jehlanu touto rovinou. Průsečíky řezu s přímkou \(p\) jsou krajní body průniku přímky \(p\) s jehlanem.

Rovina \(\delta\) na obr. 10.1 je vrcholová rovina, tzn. rovina, která obsahuje hlavní vrchol jehlanu. Konstrukce řezu jehlanu vrcholovou rovinou je obvykle jednodušší než konstrukce řezu jinou rovinou. Řezem je totiž vždy trojúhelník. Vrcholy řezu jsou hlavní vrchol jehlanu a průsečíky půdorysné stopy roviny \(\delta\) s obvodem podstavy jehlanu (za předpokladu, že podstava jehlanu leží v půdorysně).

Vrcholová rovina \(\delta\) je zadána přímkou \(p\) a vrcholem \(V\). Na obr. 10.1 je vrcholem \(V\) vedena přímka \(q\) rovnoběžná s přímkou \(p\). Průsečíky přímek \(p\), \(q\) s nárysnou (resp. s bokorysnou) prochází nárysná (bokorysná) stopa roviny \(\delta\). Nyní jsme schopni zobrazit půdorysnou stopu vrcholové roviny \(\delta\). Místo rovnoběžky \(q\) lze vést vrcholem \(V\) přímku různoběžnou s přímkou \(p\) - ideálně tak, aby se její půdorysný stopník vešel do výkresu. Dále nemusíme hledat nárysnou ani bokorysnou stopu vrcholové roviny. K řešení průniku nám postačí půdorysná stopa vrcholové roviny jako spojnice půdorysných stopníků přímek určujících rovinu.

Ani při řešení průniku přímky s tělesem nesmíme zapomenout na viditelnost. Je-li přímka vně tělesa, musíme rozhodnout, zda leží před tělesem, nebo za ním. Pokud průsečík přímky s tělesem leží ve stěně tělesa, která je vidět, přímka vycházející z tělesa tímto bodem je rovněž vidět. Pokud průsečík leží ve stěně, která vidět není, není vidět ani tento průsečík. Přímka je zde neviditelná až do části, kde její průmět vychází ven z průmětu tělesa.

Úloha 55. \(X\)[5-13; 3-20], \(\triangle XYZ\): \(|XY|=6\), \(|YZ|=7\), \(|XZ|=5\). Je dán pravidelný trojboký jehlan \(ABCV\) s podstavou v nárysně. Výška jehlanu \(v = 7\), body \(A=[4;0;3]\), \(B=[1;0;6]\) (viz úloha 40). Dále jsou dány body \(N^{q} = [7;0;6]\), \(M^{q} = [0;6;6]\). Sestrojte průnik jehlanu s přímkou \(q = \leftrightarrow N^{q}M^{q}\). ŘEŠENÍ

Průnik přímky s hranolem určujeme podobně jako průnik přímky s jehlanem. Zvolíme libovolnou rovinu, která obsahuje danou přímku, sestrojíme řez hranolu touto rovinou, a určíme body průniku. Výhodné je zvolit směrovou rovinu, tedy rovinu, která obsahuje přímky rovnoběžné s bočními hranami hranolu. Za předpokladu, že průnikem přímky s hranolem je úsečka (viz úvod kapitoly 10), řezem hranolu touto rovinou je rovnoběžník.

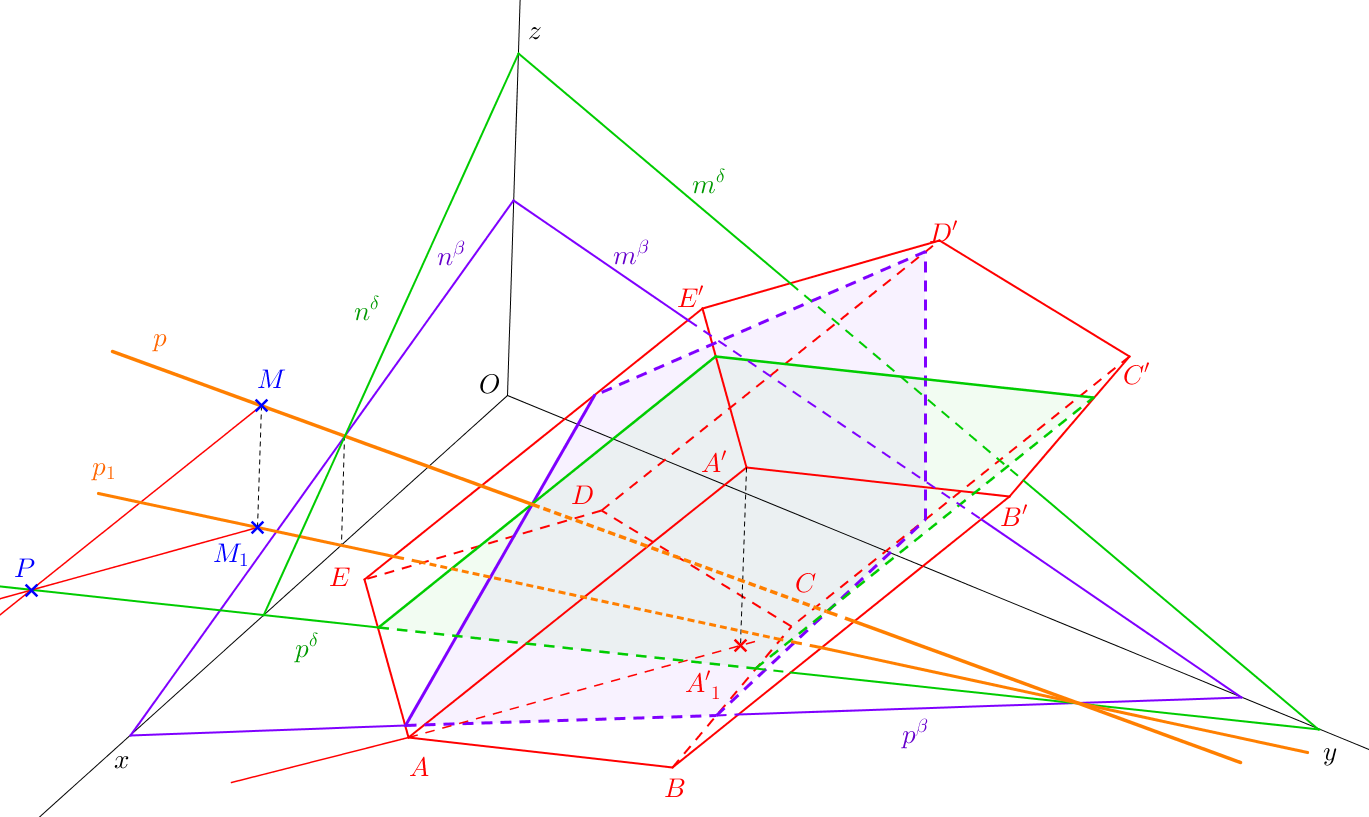
Na obr. 10.2 je zobrazen průnik přímky \(p\) s hranolem \(ABCDEA'B'C'D'E'\). Je zvolena obecná rovina \(\beta\) procházející přímkou \(p\) a sestrojen řez hranolu touto rovinou. Průnikem přímky \(p\) s hranolem je její průnik s řezem hranolu rovinou \(\beta\).

Půdorysnou stopu směrové roviny \(\delta\) najdeme tak, že libovolným bodem \(M\) přímky \(p\) vedeme přímku \(q\) rovnoběžnou s boční hranou hranolu. Půdorysnými stopníky přímek \(q\) a \(p\) proložíme půdorysnou stopu \(p^\delta\) roviny \(\delta\). Půdorysná stopa \(p^\delta\) určí stranu řezu, která leží v dolní podstavě hranolu. Další dvě strany řezu jsou rovnoběžné s bočními hranami hranolu a prochází průsečíky stopy \(p^\delta\) s podstavnými hranami hranolu. Poslední strana řezu leží v horní podstavě hranolu a je rovnoběžná s půdorysnou stopou roviny \(\delta\).

Úloha 56. \(X\)[4-10; 5-16], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán pravidelný šestiboký hranol \(ABCDEFA'B'C'D'E'F'\) jehož podstava leží v bokorysně. Bod \(A=[0;4;3]\), střed podstavy \(S=[0;4;6]\), výška hranolu \(v = 7\) (viz úloha 37). Dále jsou dány body \(N^{m}=[5;0;5]\), \(M^{m}=[0;9;7]\). Sestrojte průnik hranolu s přímkou \(m = \leftrightarrow N^{m}M^{m}\). ŘEŠENÍ

Úloha 57. \(X\)[5-8; 3-19], \(\triangle XYZ\): \(|XY|=7\), \(|YZ|=8\), \(|XZ|=9\). Jsou dány body \(A=[4;0;2]\), \(B=[4;0;6]\), \(C=[7;0;8]\), \(K=[8;8;8]\), \(L=[6;4;2]\) a délka \(v=9\). Sestrojte průnik přímky \(KL\) s kolmým hranolem \(ABCA'B'C'\). Výška hranolu je \(v\).

10.2 Průnik přímky s rotačním tělesem

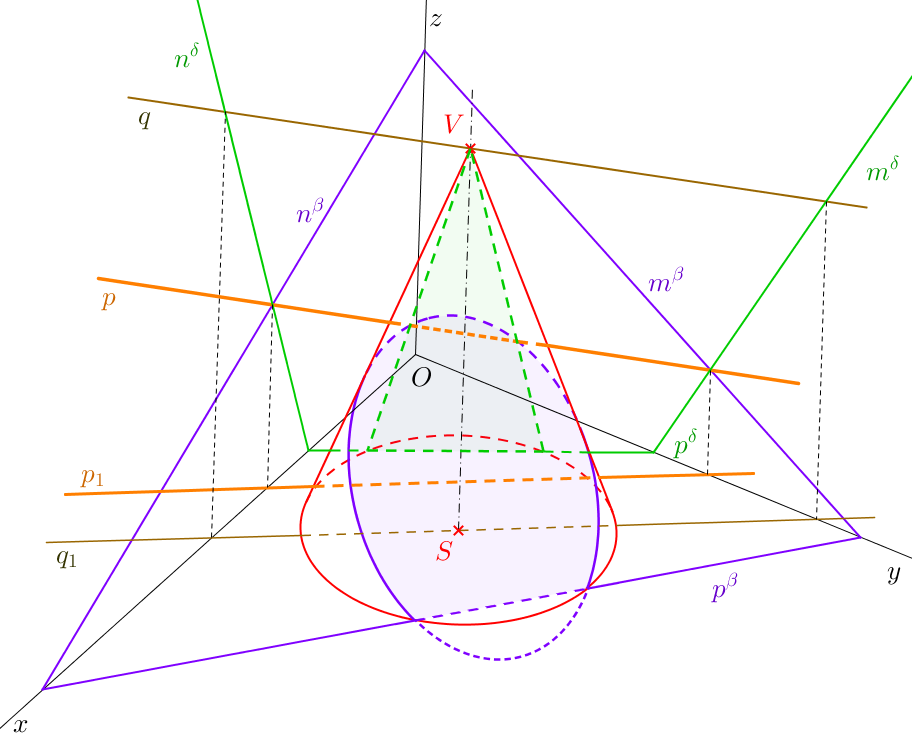
Průnik přímky s rotačním tělesem najdeme stejně jako průnik přímky s mnohostěnem: zvolíme rovinu, která danou přímku obsahuje, a sestrojíme řez tělesa touto rovinou. Průnikem přímky s tělesem je její průnik s řezem. Vzhledem k obtížnější konstrukci řezu je ale nevýhodné volit u válců/kuželů jinou rovinu, než směrovou/vrcholovou (obr. 10.3 a 10.4).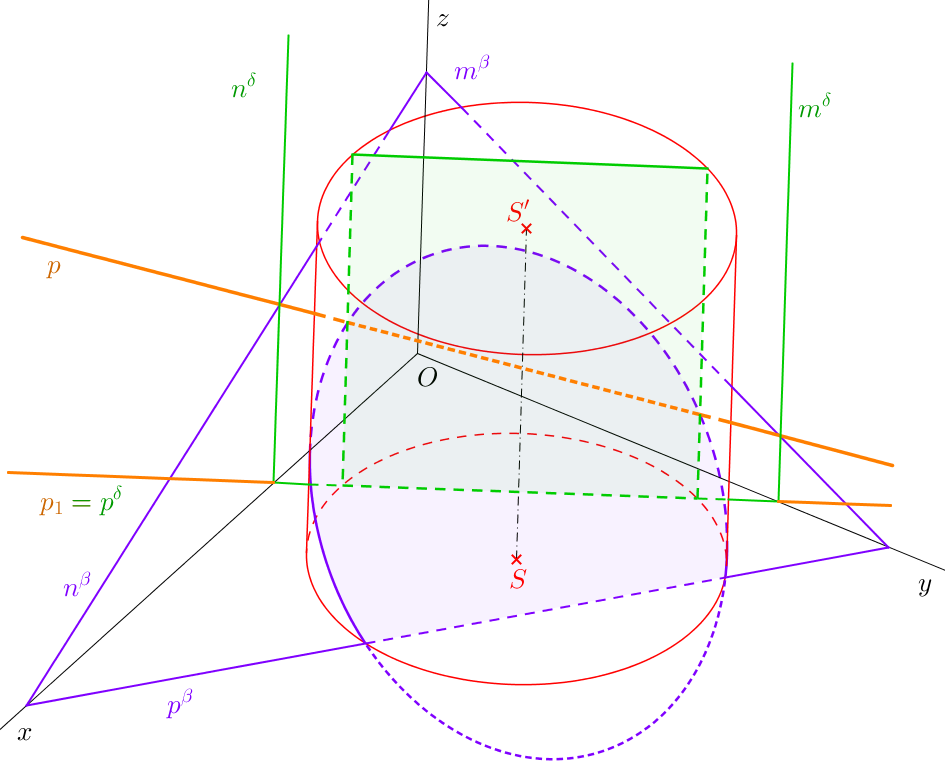

Na obr. 10.3 je zobrazen průnik přímky \(p\) s rotačním válcem. Můžeme si všimnout dvou různých řezů. Řez obecnou rovinou \(\beta\) vede k řešení průniku, konstrukce řezu je ale velmi náročná (je třeba sestrojit elipsu a následně průsečíky elipsy s přímkou). Při volbě směrové roviny \(\delta\) je řezem rotačního válce obdélník (zobrazí se jako kosodélník). Vyhneme se tak konstrukci kuželosečky.

Úloha 58. \(X\)[7-12; 7-19], \(\triangle XYZ\): \(|XY|=4\), \(|YZ|=5\), \(|XZ|=6\). Je dán rotační válec, jehož podstava se středem \(S = [8;8;0]\) a poloměrem \(r=3\) leží v půdorysně, výška válce je \(v=7\) (viz úloha 43). Dále jsou dány bod \(N=[6;0;7]\), \(L=[8;9;3]\). Sestrojte průnik válce s přímkou \(k = \leftrightarrow NL\). ŘEŠENÍ

Úloha 59. \(X\)[4-9; 6-19], \(\triangle XYZ\): \(|XY|=9\), \(|YZ|=9\), \(|XZ|=9\). Jsou dány body \(S=[2;0;1]\), \(K=[4;2;1]\), \(L=[1;1;8]\) a délky \(r=6\), \(v=5\). Sestrojte rotační válec, jehož podstava se středem \(S\) a poloměrem \(r\) leží v nárysně. Výška válce je \(v\). Sestrojte průnik válce s přímkou \(KL\).

Řešení průniku přímky \(p\) s kuželem vidíme na obr. 10.4. Jednou možností je použít libovolnou rovinu \(\beta\), jejímž řezem je kuželosečka, kterou následně musíme sestrojit, abychom našli průnik přímky s kuželem. Nebo můžeme přímkou \(p\) proložit vrcholovou rovinu \(\delta\). Řezem kužele rovinou \(\delta\) je trojúhelník.

Úloha 60. \(X\)[3-9; 2-18], \(\triangle XYZ\): \(|XY|=8,5\), \(|YZ|=8\), \(|XZ|=5\). Je dán rotační kužel s podstavou v půdorysně. Střed podstavy \(S=[0;0;0]\), poloměr podstavy \(r=3\), výška kužele \(v=10\) (viz úloha 45). Dále jsou dány body \(M=[0;4;6]\), \(N=[1;0;4]\). Sestrojte průnik kužele s přímkou \(l=\leftrightarrow MN\). ŘEŠENÍ

Ukažme si ještě průnik osy \(x\) s koulí, jejíž střed je v počátku \(O\) (obr. 10.5). Mohli bychom sestrojit řez koule půdorysnou či nárysnou a najít průnik s osou \(x\) pomocí tohoto řezu. Tím bychom si ale zbytečně zkomplikovali práci. Uvědomme si, že průsečíky přímky s povrchem koule leží na ose a jejich vzdálenost od středu koule je poloměrem koule. Stačí tedy do axonometrické průmětny sklopit promítací rovinu osy \(x\) nebo otočit půdorysnu/nárysnu. Ze sklopení (otočení) přeneseme skutečnou délku poloměru na axonometrickou osu \(x\).